May 16, 2022 / 8 /

Thevenin's Theorem Explained With Solved Examples

Thevenin theorem is a theorem used to model complex circuits into a simple circuit with an equivalent voltage source and resistance.

As the theorem states that;

‘any two terminals of a network can be replaced by an equivalent voltage source and an equivalent series resistance.

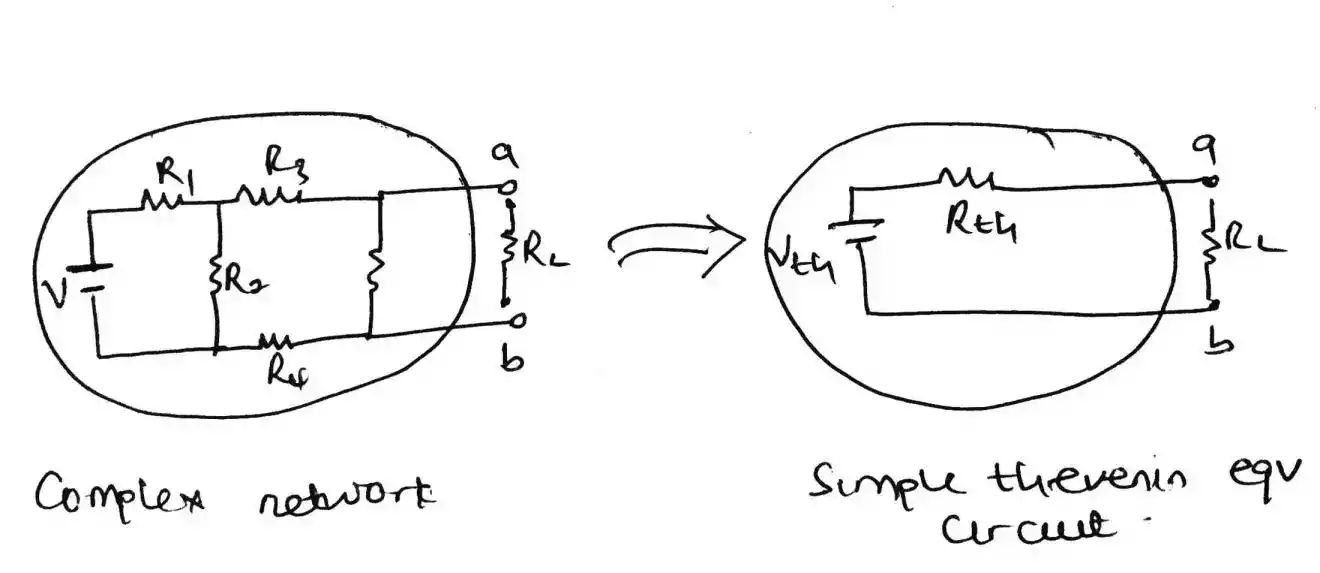
The voltage source is the voltage across the two terminals with load, if any, removed.

The series resistance is the resistance of the network measured between two terminals with load removed and constant voltage source being replaced by its internal resistance (or if it is not given with zero resistance, i.e., short circuit) and constant current source replaced by infinite resistance, i.e., open circuit.’

But why do we need this theorem

Because it is not like mesh analysis or nodal analysis which we use to analyze circuit but rather it is a technique that makes engineers unique (to my opinion). Here’s is what I mean, if two engineers are tasked to design a circuit each with an output of (5V and 1A).

The first engineer let’s say MR X decided to design his own circuit with 2 resistors and a 20V battery as shown below while MR Y decided to design his own circuit with just one resistor and a 9V battery as shown below also.

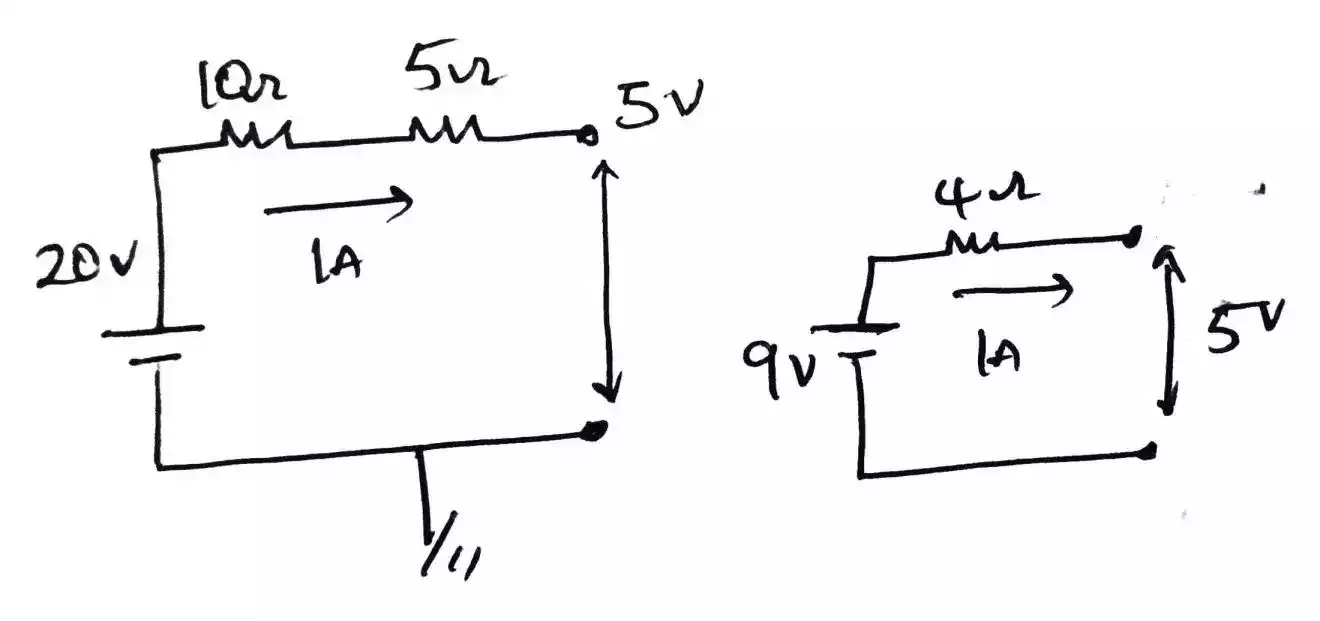
As you can see, both circuit gives the required output but what both circuits contain are different and this is what makes the thevenin theorem helpful as it lets us to approximately guess what another engineer has designed even if one does not know what is inside the box containing the circuit just as our home charger.

There are different variations but at the end of the day, the output of those charger are quite same.

Steps to solve circuit problem using thevenin theorem

1. If there is a load resistor R_L then you need to remove it.

2. Find the thevenin voltage V_th across the terminal of interest. The V_th can be found by finding the open circuit voltage across the terminal

3. Find the short circuit current I_sc between terminal a → b

4. With the short circuit current known, the thevenin resistance can be found by dividing V_th by I_sc

   To solve for V_th, you can use whatever technique you are most comfortable with or that suit the problem at hand maybe mesh analysis, nodal analysis or source transform.

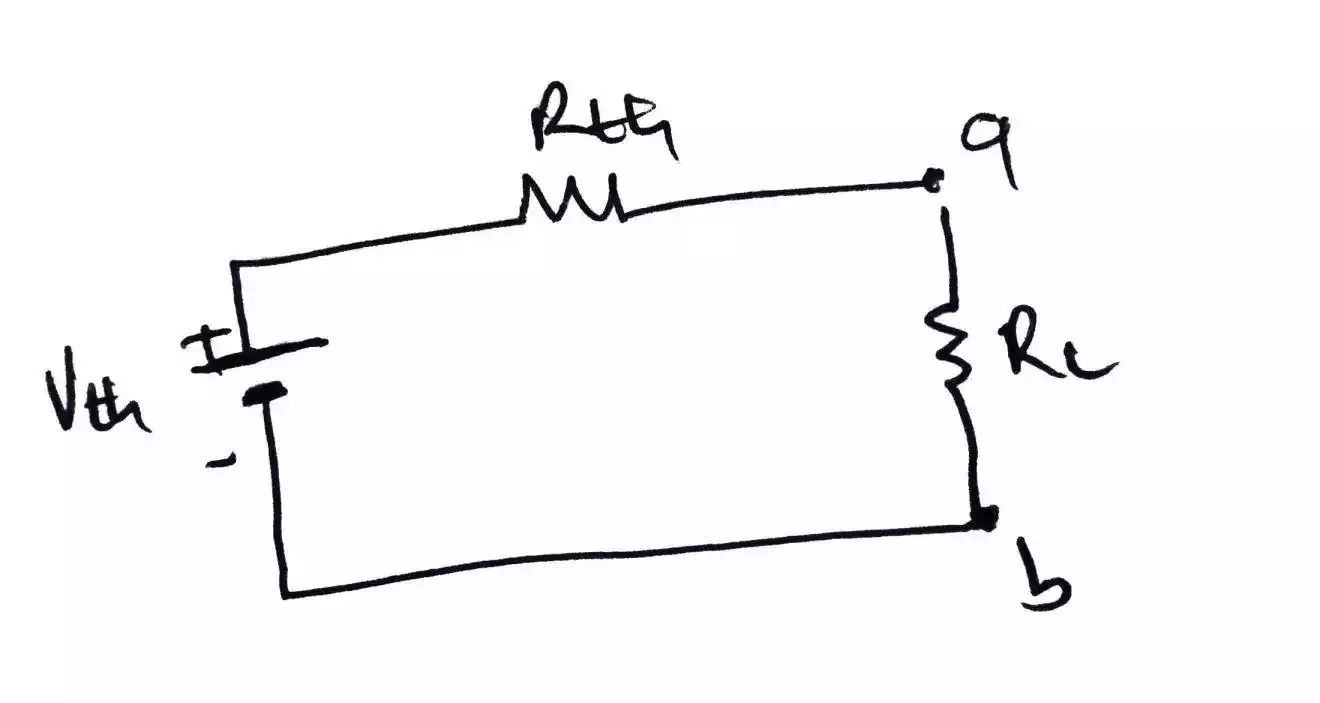
   After finding the V_th and R_th then you need to sketch your circuit as shown below.

   

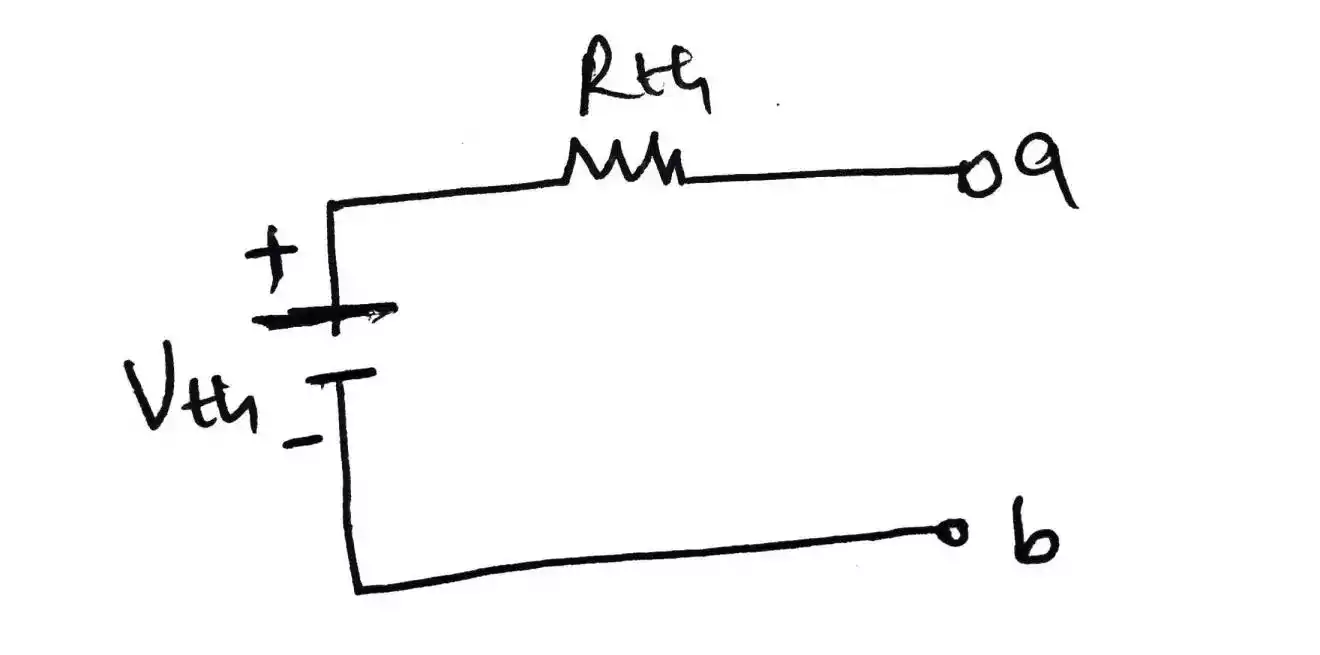
   Also if there is R_L then, you need to replace the open terminal a → b with R_L as shown below and lastly find the current that flow through R_L as the current that flows through it is not I_sc.

Lets solve some examples to understand the concept better.

Example problem on thevenin’s theorem

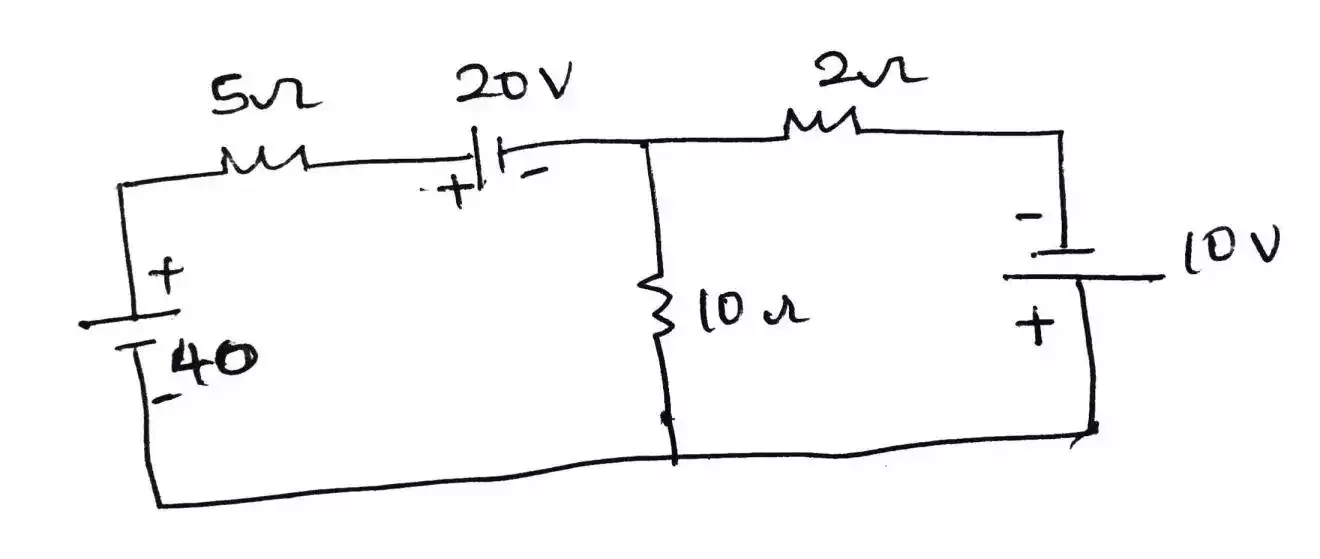
Ex.1 – find the current through the 2Ω resistor using thevenin theorem?

Step 1:

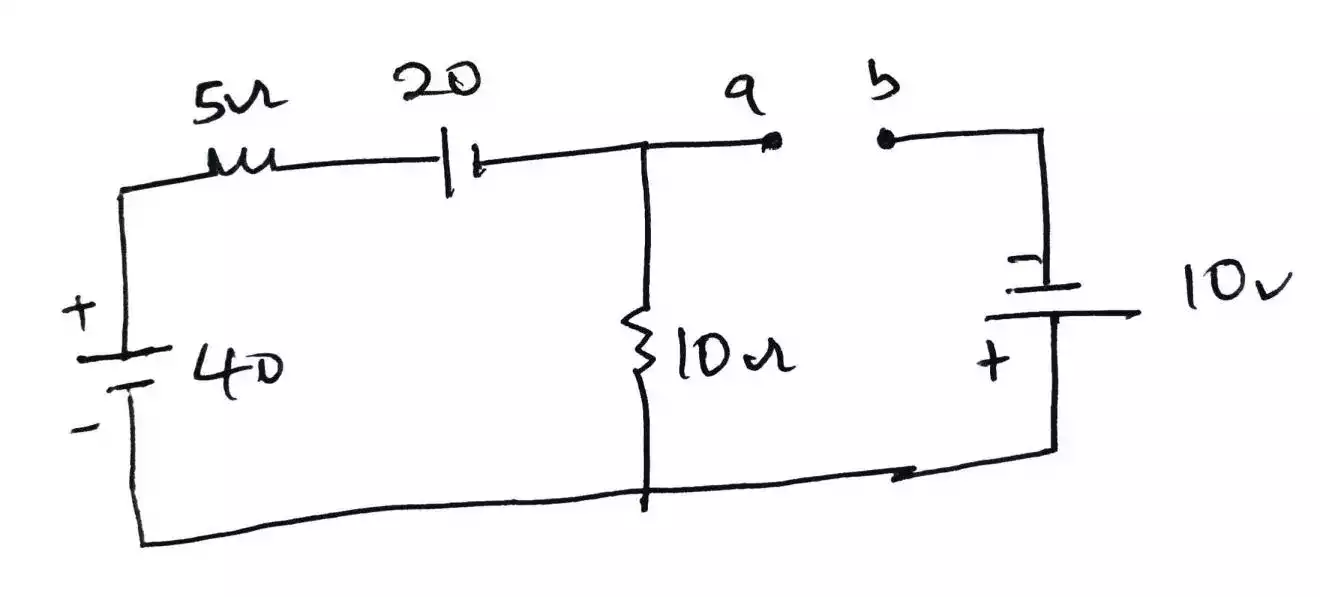
Remove the 2Ω resistor and leave the terminal open.

Step 2:

Using mesh analysis, lets analyse the circuit. Since there is only one loop as the terminal a → b has made the second loop to no longer be a loop.

The equation gotten is :

40-5i-20-10i = 0

20-15i = 0

15i=20

I=20/15 = 1.33A.

Now to find the open terminal voltage V_th, we need to add the voltage across the 10Ω resistor and the 10V battery.

Thus, the voltage across the 10Ω is V_10Ω = 10 * 1.33 = 13.3v

Hence, V_th = 13.3 + 10 = 23.3v

Step 3:

To find I_sc we need to short circuit the a → b terminal.

Now since short circuiting of the circuit has cause the loop to be two as oppose to one that we previously did.

So equation for loop I:

40- 51₁-20-10(1₁-1₂) =0;

40-51₁-20-101₁+101₂ =0; by expanding the bracket

20-151₁+101₂ = 0;

151₁-101₂=20 ………(1)

Loop II

-10(1₂-1₁)+10 =0;

-101₂+101₁+10 =0;

101₁-101₂=-10……………..(2)

By solving the simultaneous equation, we get

1₁ = 6A;

1₂ = 7A;

But I_sc = 1₂ = 7A

hence, R_th = V_th/I_sc = 23.3/7 = 3.33Ω

now replacing the 2Ω resistor we removed earlier then the circuit becomes this;

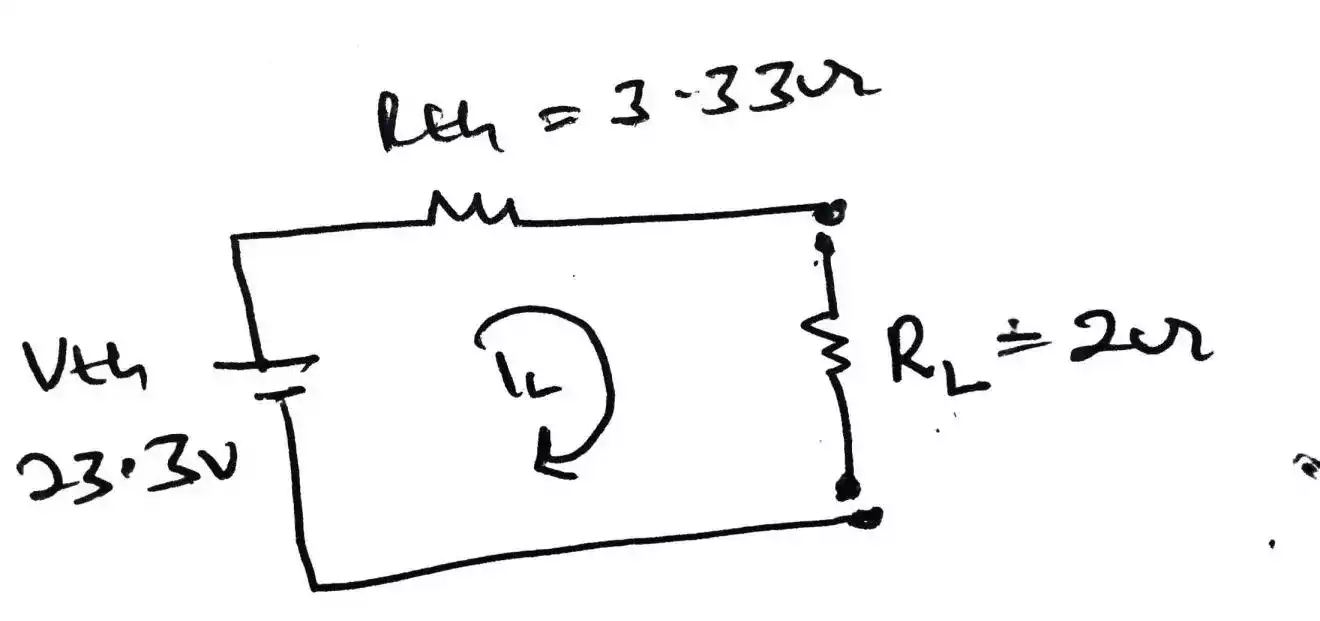
but we need to calculate for the current that flows through the load resistor (2Ω),

I_L = V_th / (R_th + R_L) = 23.3/(3.33 +2) =23.3/(5.33) = 4.37A