October 22, 2021 / 7 /

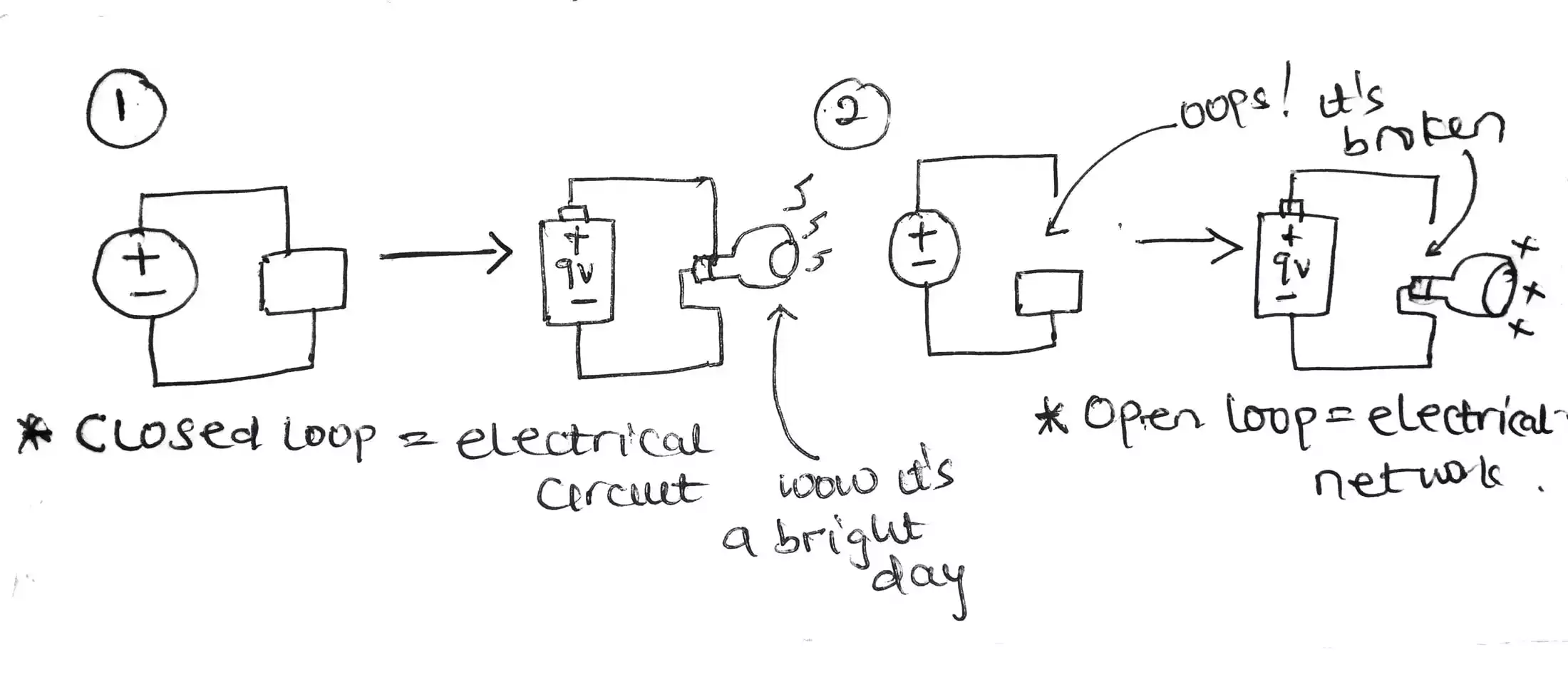
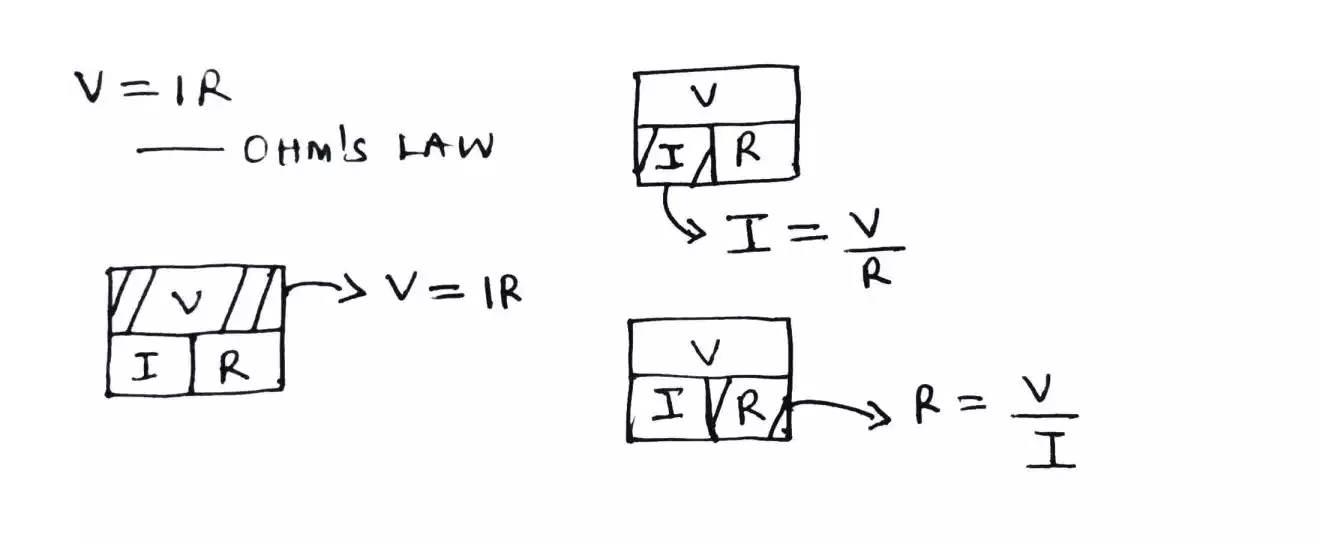
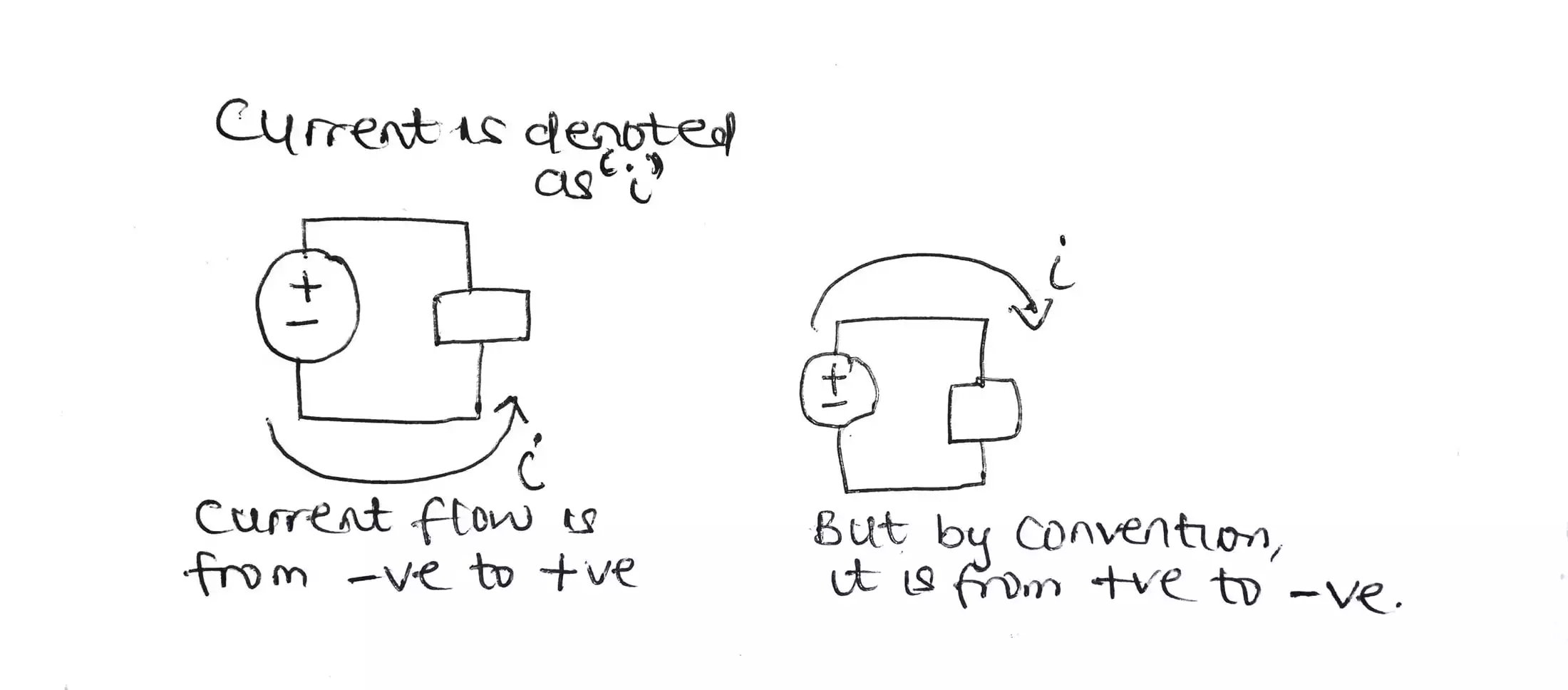
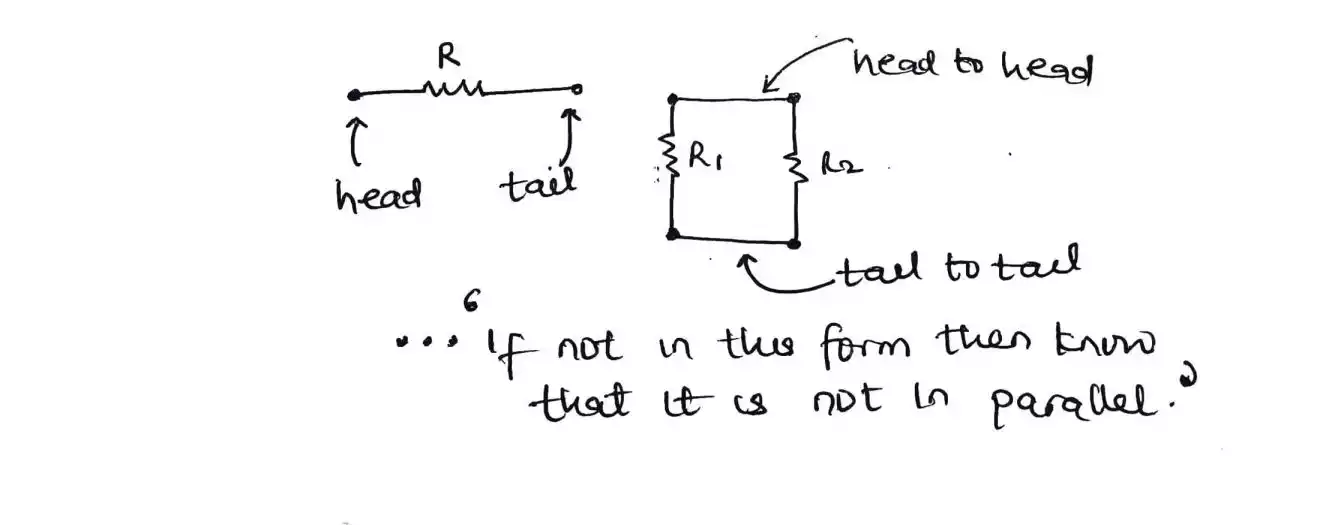
Kirchhoff’s current and voltage law explained with steps to solving any circuit problems easily

Before diving into what the Kirchhoff’s law is, can you solve this circuit using ohm’s law to find all the currents flowing in each branch of the circuit.

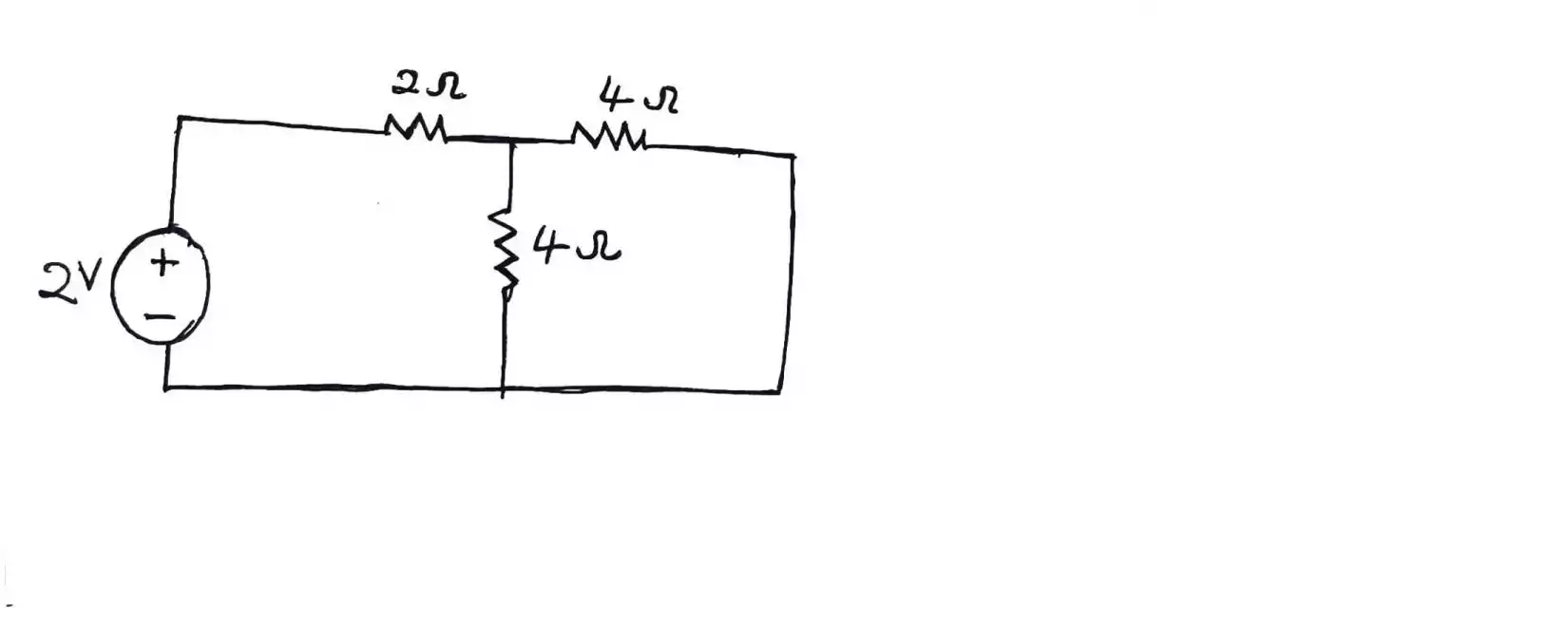
I probably know it will be frustrating to solve this circuit using ohm’s law because there are more than one connection of resistors and also more than one loop which means ohm’s law won’t be a perfect technique to use

Rather, we need an optimized technique which still is based on ohm’s law (as ohm’s law is the base that relates voltage, current and resistance) but it is a little bit easier to work with.

This optimized technique is called Kirchhoff’s law.

Kirchhoff’s law has two laws within it which are called Kirchhoff’s current law or KCL and Kirchhoff’s voltage law or KVL.

What is Kirchhoff’s current law or KCL

Kirchhoff’s current law states that the algebraic sum of currents at a node is equal to zero.

In other words, the total amount of current entering a node is equal to the total amount of current leaving the node.

And if we algebraically sum the current entering (which is considered positive) and the current leaving (which is considered negative) as shown above, we get zero as the equivalent result.

Remember

Kirchhoff's Current Law is applied at nodes or junction point.

Terminology

**Node** - A node is a junction where two or more network elements are connected together.

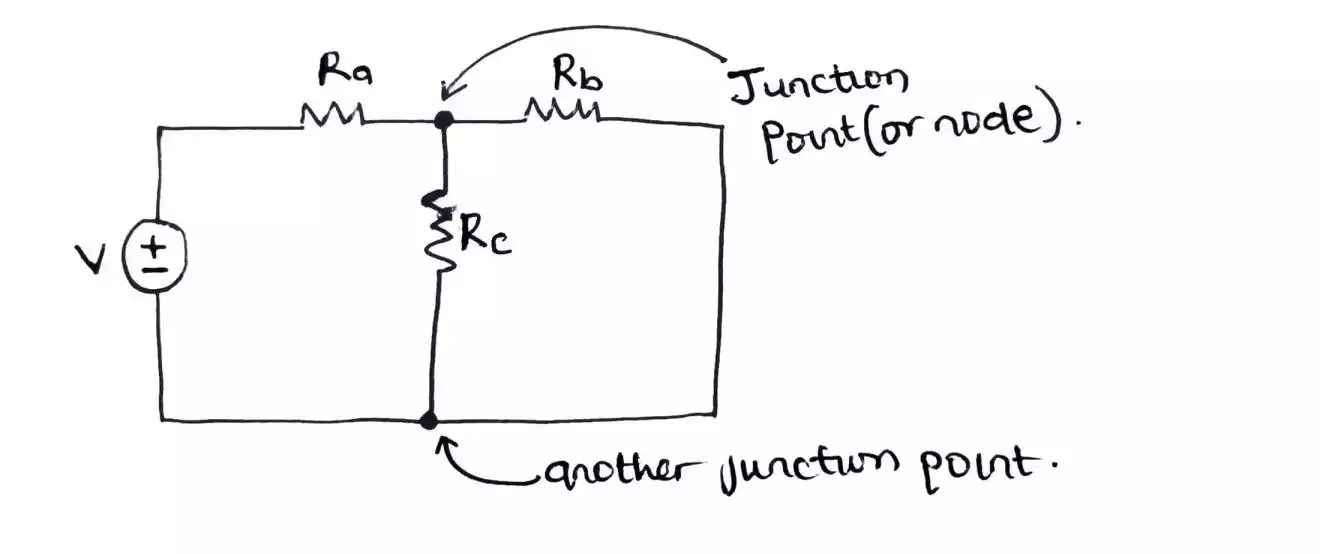
What is Kirchhoff’s voltage law or KVL

Kirchhoff’s voltage law states that the algebraic sum of all the voltages in any closed circuit is zero.

In other words, if we start to move round any closed path or loop, the total sum of all the voltages across each element in the circuit is zero.

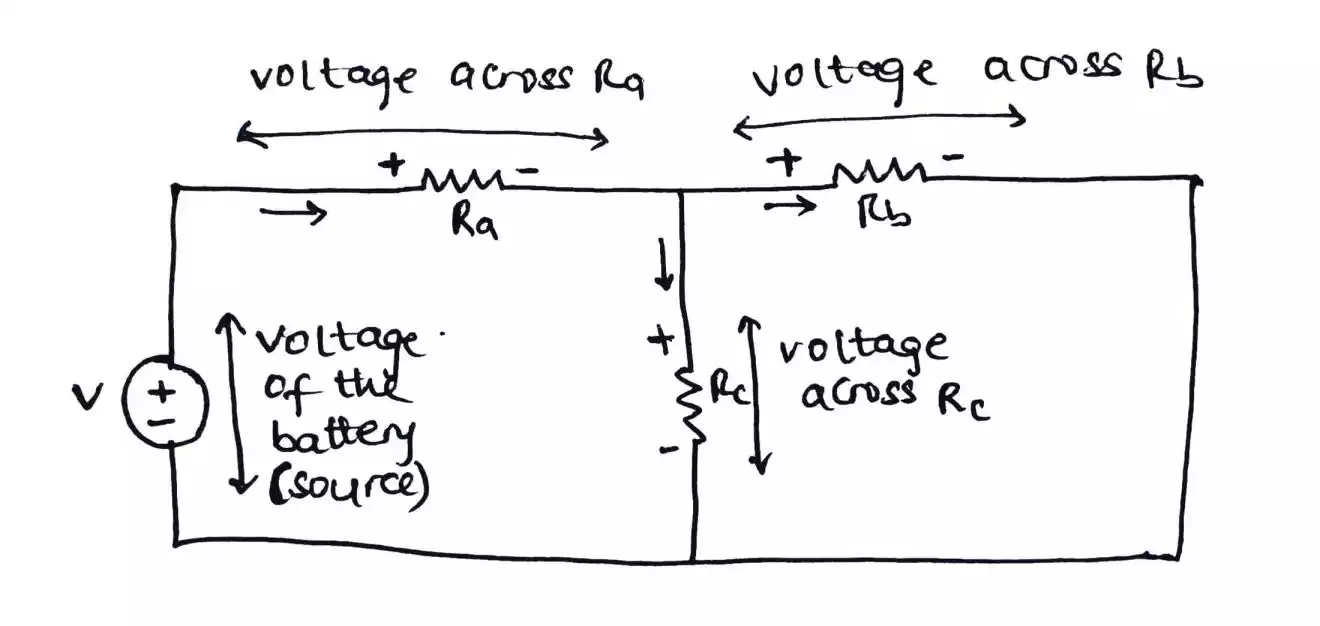
Remember

Kirchhoff's Voltage Law is applied around a closed loop hence, it deals with branches.

Terminology Branch - An element or number of elements connected between two nodes constitute a branch. Loop - A loop is any closed part of the circuit.

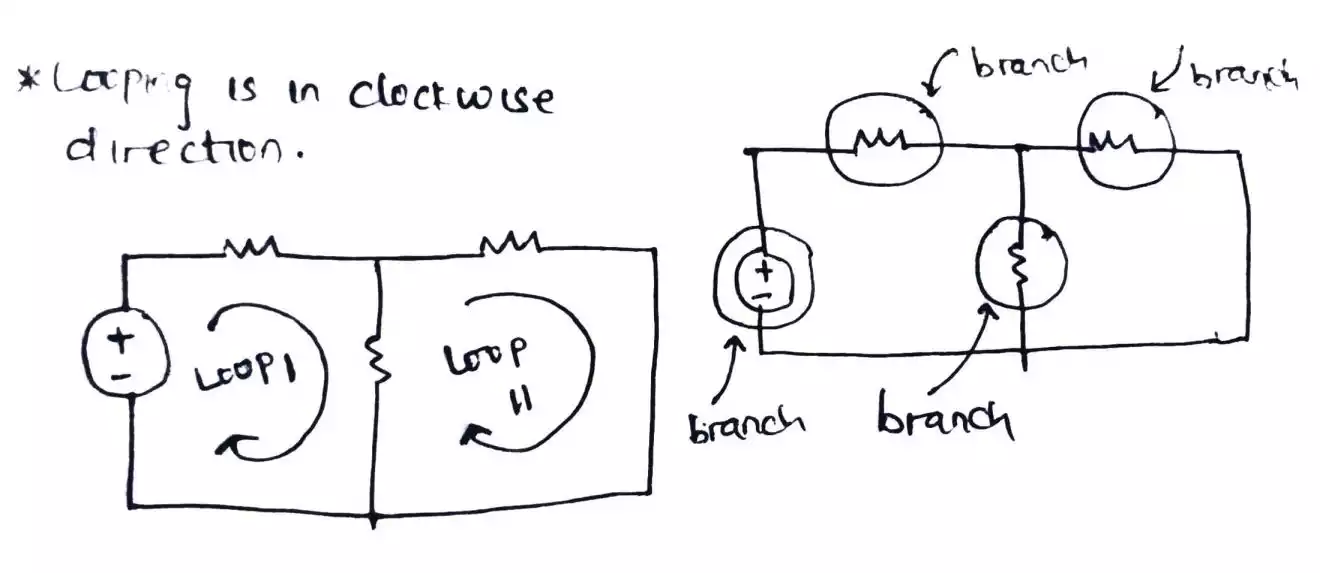
How to solve circuit problems using kirchhoff’s law

Let’s solve some example to see how this laws are implemented.

Example 1.

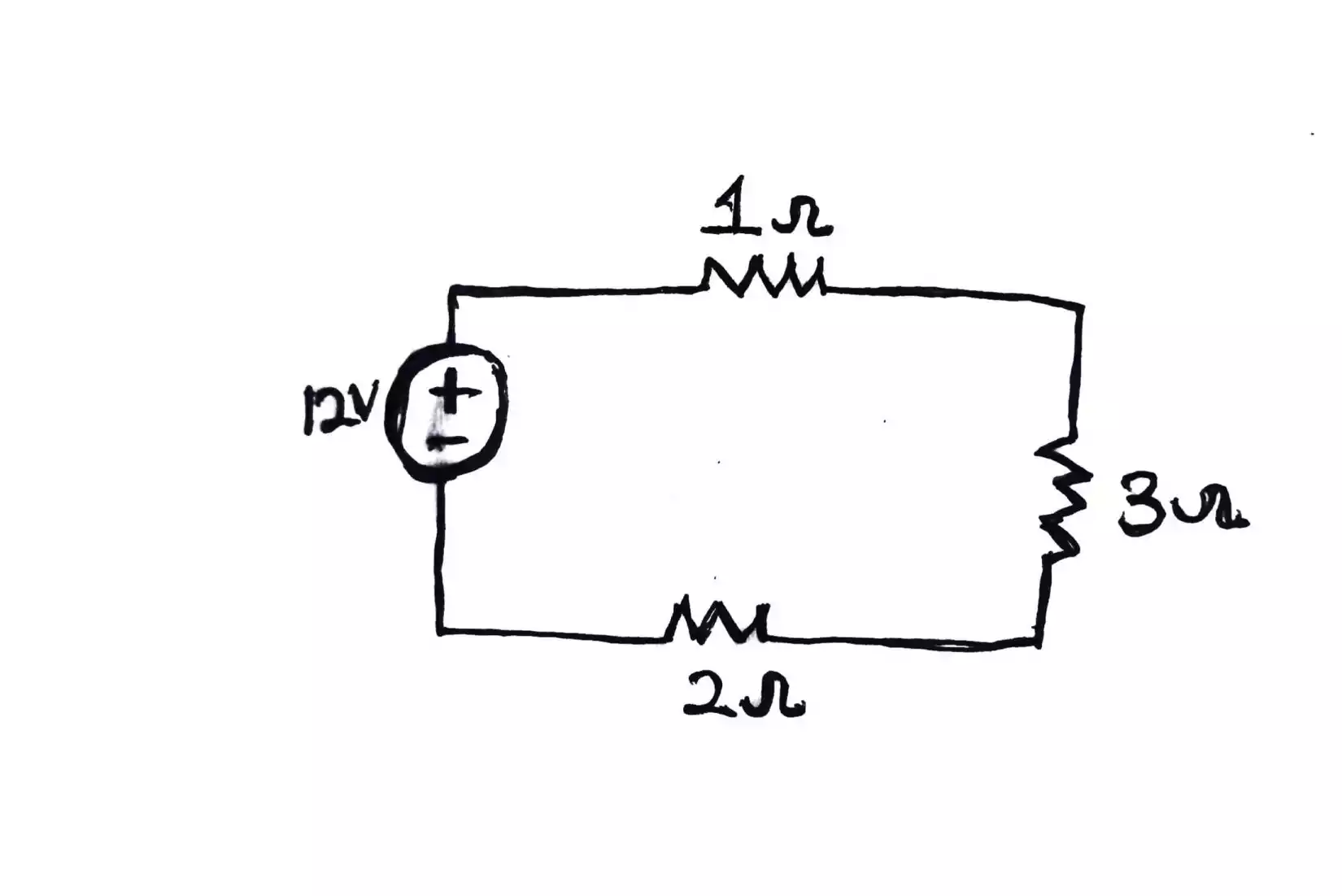
The question asks us to use Kirchhoff’s law to find the current flowing in the loop as well as the voltage drops across each resistor, 1Ω, 3Ω and 2Ω.

Here are the simple steps to help solve this circuit problem and even other circuit problems.

Step 1

Check how many loop is present. Because this is one of the mistakes students make while solving circuit problems using Kirchhoff’s law.

After finding how many loop is present then, the current you are to find will be based on the number of the loops.

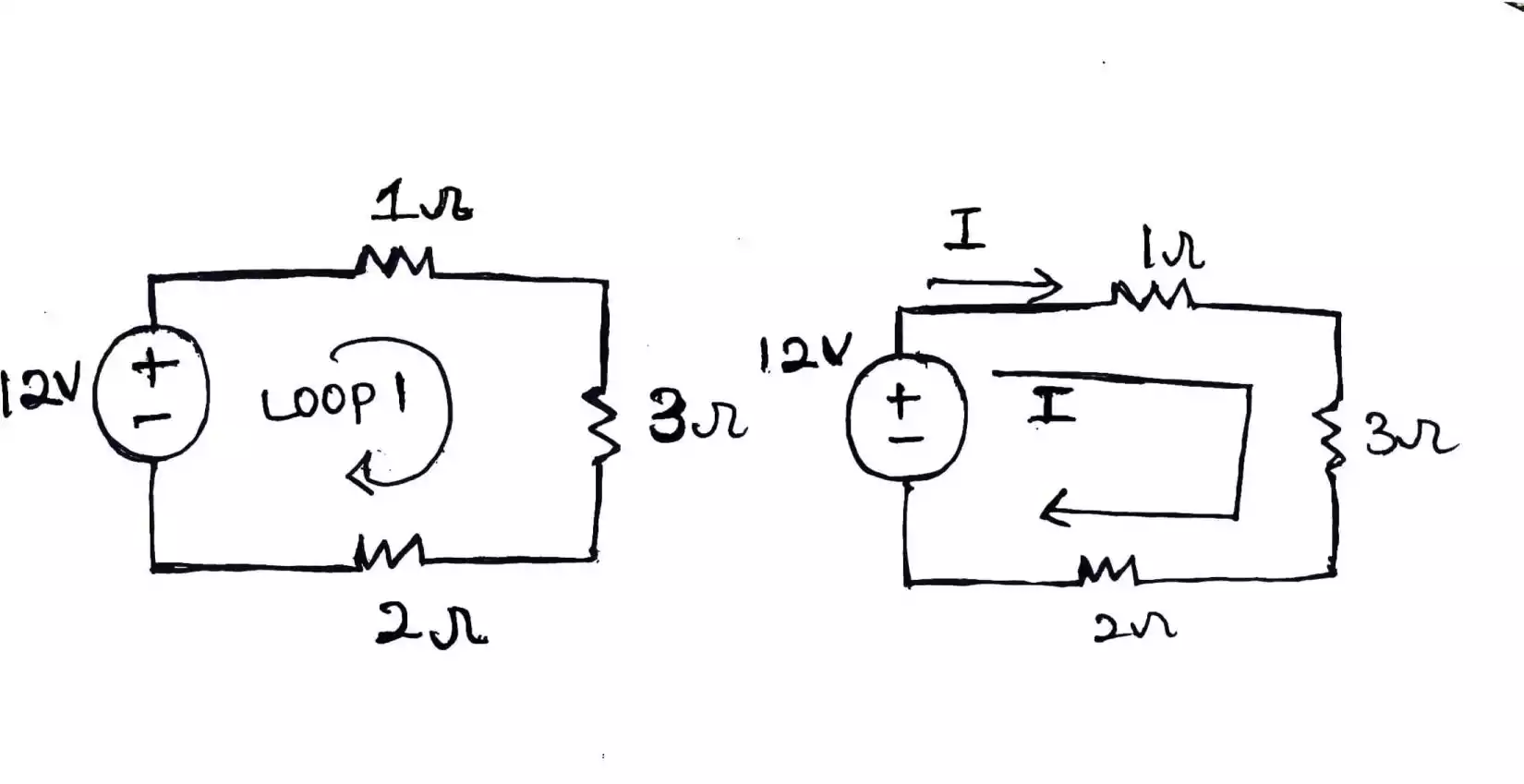
i.e. if there is one loop as in the case of our circuit problem, we just need to define one current. Which means if there are more loops let say two loops, then we need to define two currents.

Step 2.

We need to distribute the currents using KCL principle but since this example consist of only one loop then we need only one current and we define it to be I or I₁.

The reason why there is only one loop is that the resistors are connected in series and as you know for series connected resistor, the same current flow through them.

Step 3.

Distribute sign of voltage across the resistors. If you don’t know how, I will guide you through but still I recommend you to read on the article ohm’s law.

To distribute the voltage-sign across, we need to follow the direction of current in the circuit. since current is flowing from the positive side of the battery, it first sees the resistor R_1Ω and mark it input as positive, and after flowing through the resistor R_1Ω it marked negative at the outside or other end since energy is reduced or is consumed by R_1Ω.

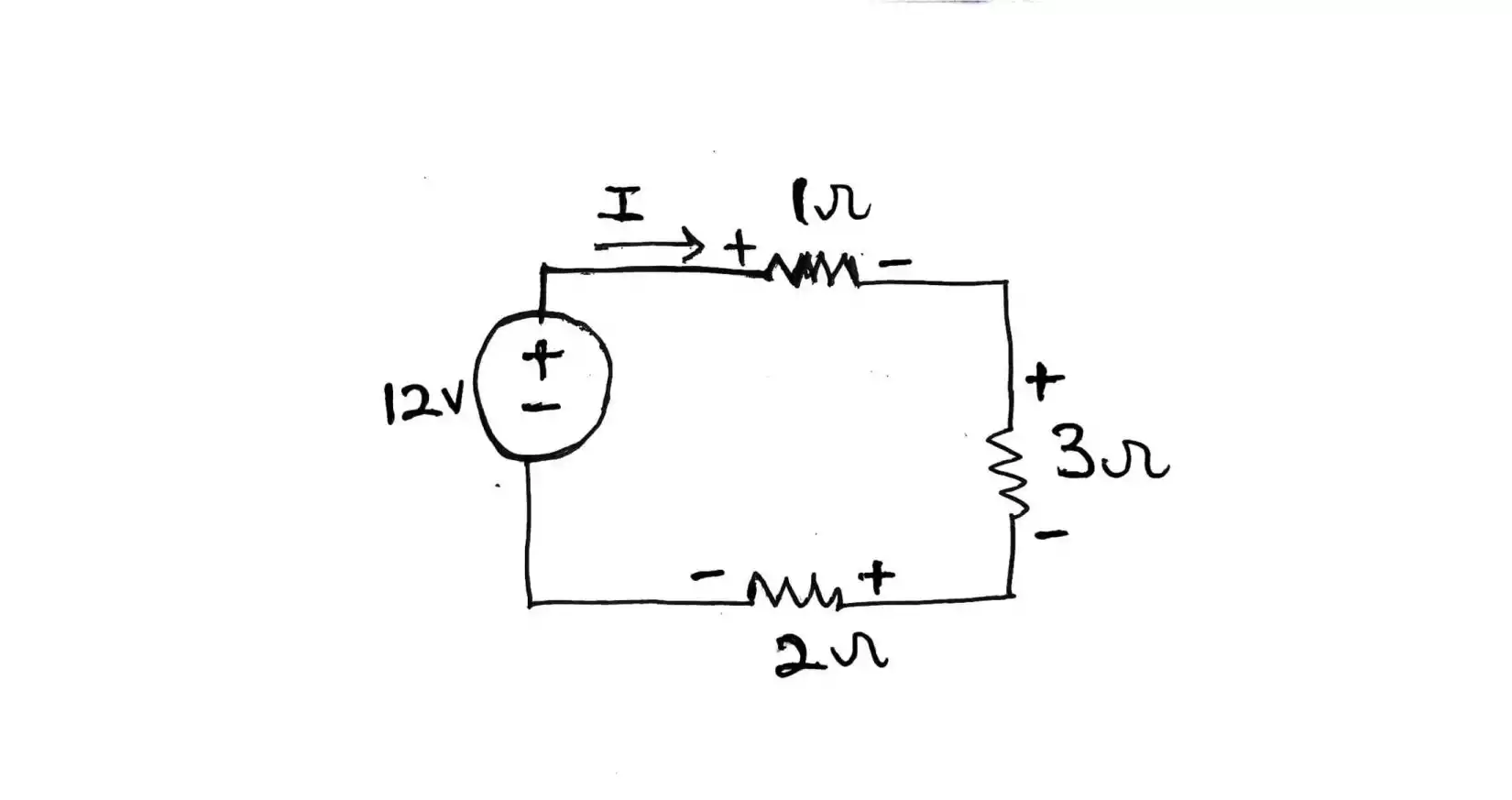
The next resistor R_3Ω sees a current coming out of R_1Ω but since this is the first time R_3Ω will be seeing the current, it marked its input as positive and as it flows through the R_3Ω, energy is reduced again and the end part is marked as negative and the same goes for the last resistor R_2Ω.

Note

If there are more resistors, the same pattern go for each.

** Step 4**
We need to start writing loop equation using ** V = IR** and then summing things up according to KVL.

Note I

Looping is done in clockwise direction but still can be done in anti-clockwise but just stick to one.

Note II

When looping through, whatever sign you encounter first is what write you down to make things easier.

The loop equation is shown below and it consist of all the voltages in the loop including the energy source or battery since it is supplying the circuit an energy.

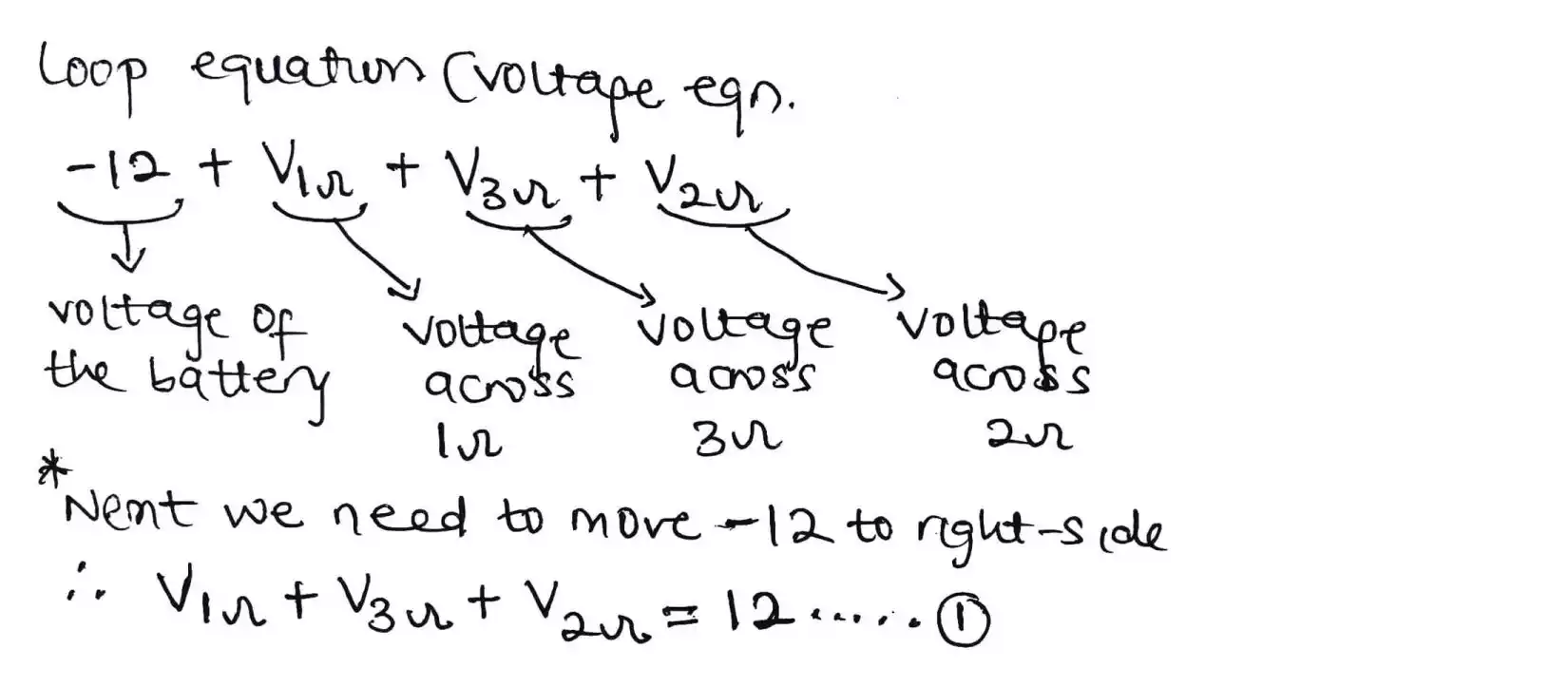
-12 + V_1Ω + V_3Ω + V_2Ω = 0

Now we need to move -12 to the other side to make it positive.

V_1Ω + V_3Ω + V_2Ω = 12 …. (1)

But V = IR and we only know what the resistance are and the current which we are looking for is the unknown.

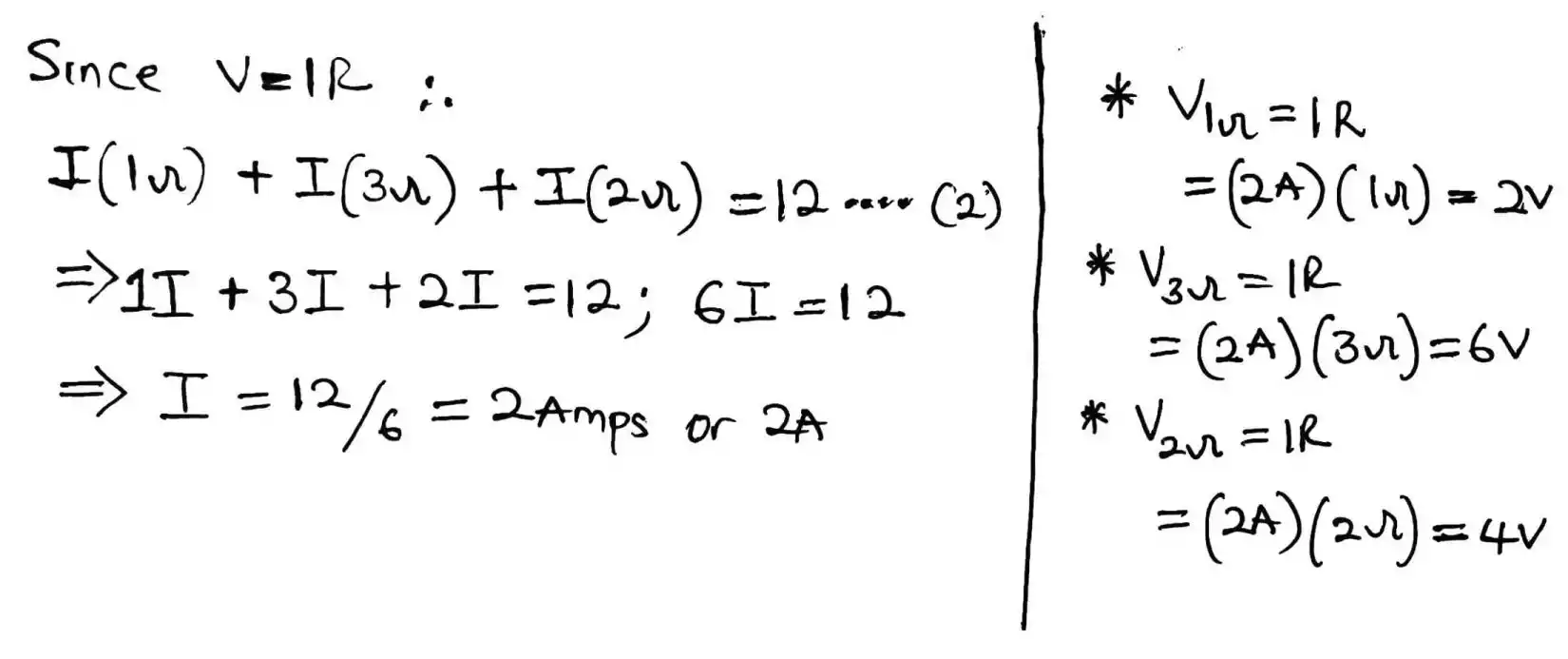
So, I x (1Ω) + I x (3Ω) + I x (2Ω) = 12 …. (2) or rewritten as 1I + 3I + 2I.

By applying basic algebra to adding 1I + 3I + 2I you will get 6I.

Therefore, 6I = 12; dividing both side by 6 to find I, I = 12/6 = 2A.

Meaning two amps of current is flowing through the circuit where by

V_1Ω = IR = (2)(1) = 2V

V_3Ω = IR = (2)(3) = 6V

V_2Ω = IR = (2)(2) = 4V

Adding V_1Ω + V_3Ω + V_2Ω you will get 2 + 6 + 4 = 12V same as the voltage of the battery.

Let’s see another problem and how you can approach solving it.

Example 2.