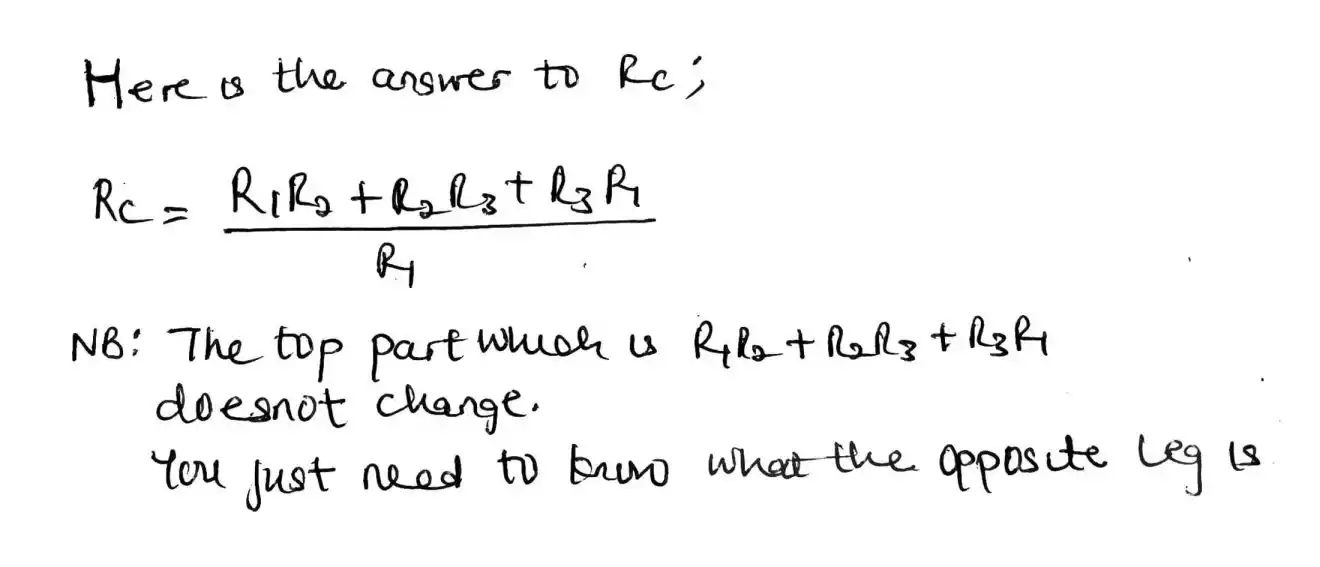Star - Delta Transformation Explained With Tips On How To Recall The Formulas

Why and how do we do star to delta or delta to star transformation

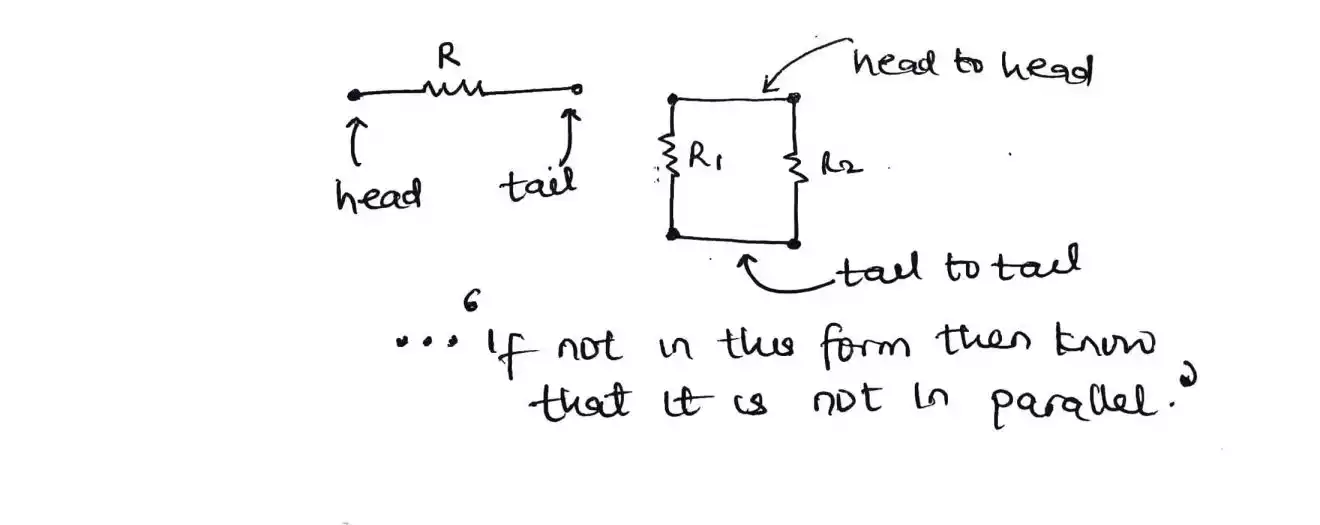
The star and delta transformation involves converting from star to delta or delta to star and we do this when our resistors are not connected in parallel or series.

This technique is quite useful but most time student do forget the formula to be used quickly but, in this section I will give you a visual tip to never forget this so let’s start.

The way delta and star are connected is illustrated below with a comparison with that of series and parallel connection of resistors.

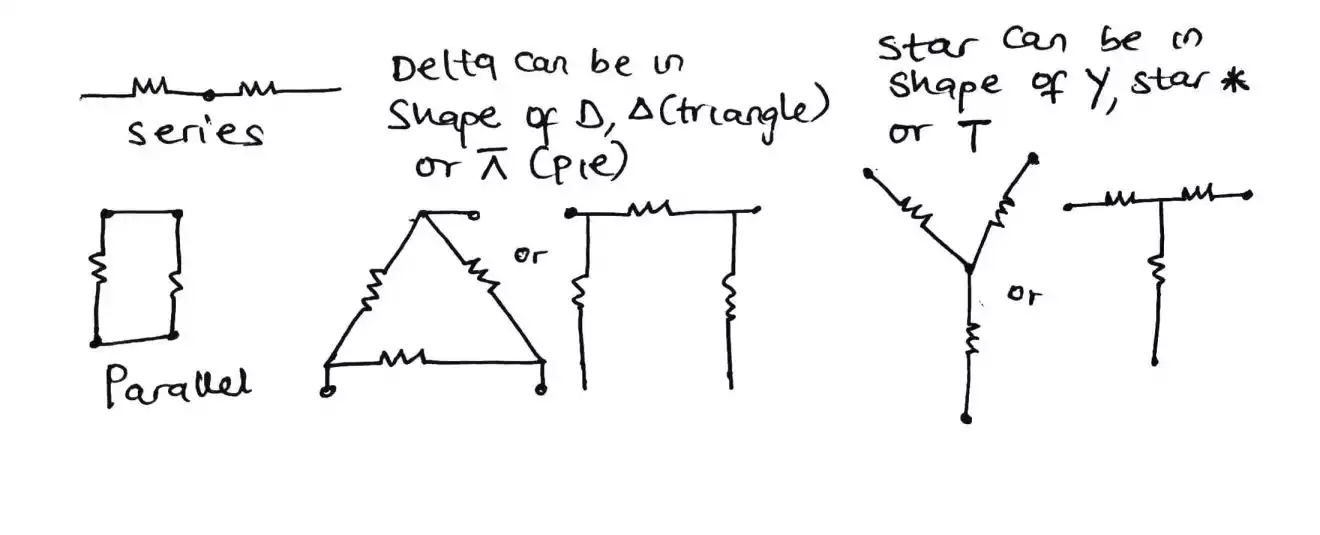
The delta can be structured in two ways as having a triangle shape or pie shape while the star has a wye or T shape so make sure to note that.

Small nugget

The star is sometimes referred to as wye while delta is referred to as pi.

The transformation or conversion from delta to star

While we will be solving circuits, sometimes we would encounter resistors connected in a form that’s not easier to work with except that we transform it to another form and then solve, so that’s why we perform this conversion.

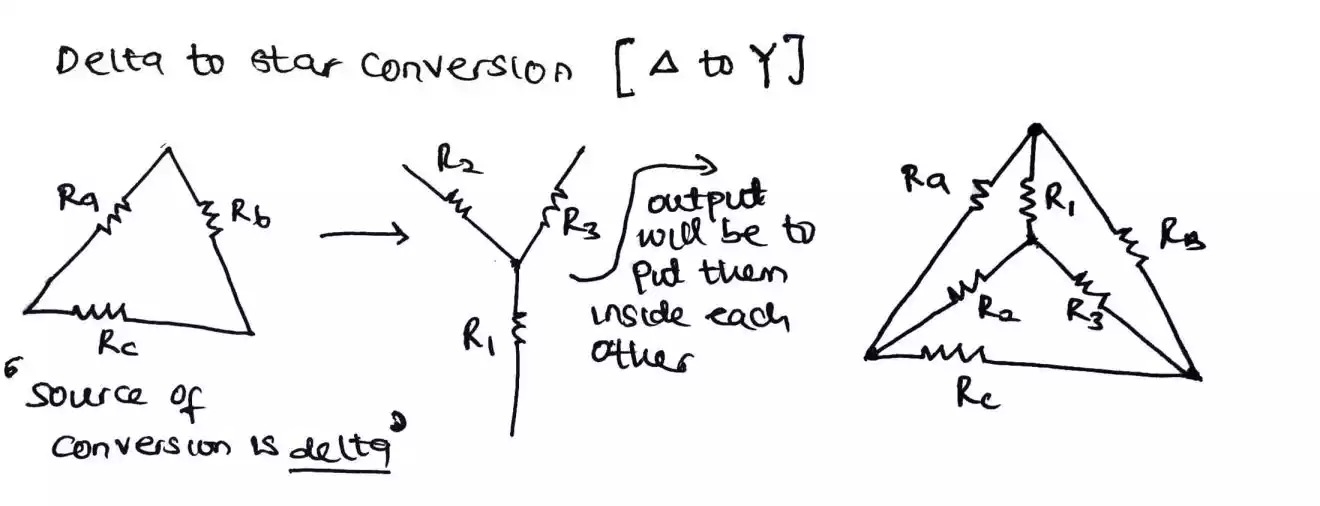
So to convert delta to star, it is done as follows, though the formula is stated as -

The formula for delta to star conversion

How to remember the formula for delta to star conversion

So let’s recall this formula by starting with R₁.

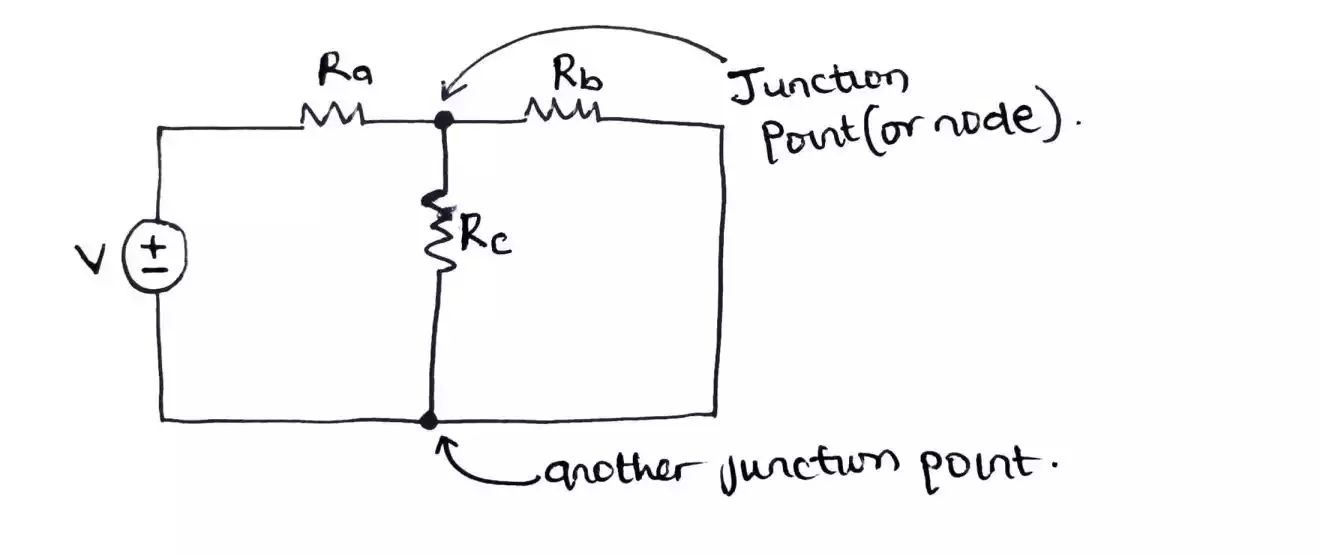
Looking at R₁, we can see that the node at the top of R₁ has two resistors from the delta network, connected or tied to it. So in that case, we say that there are 2 legs affecting R₁ which are R_a and R_b.

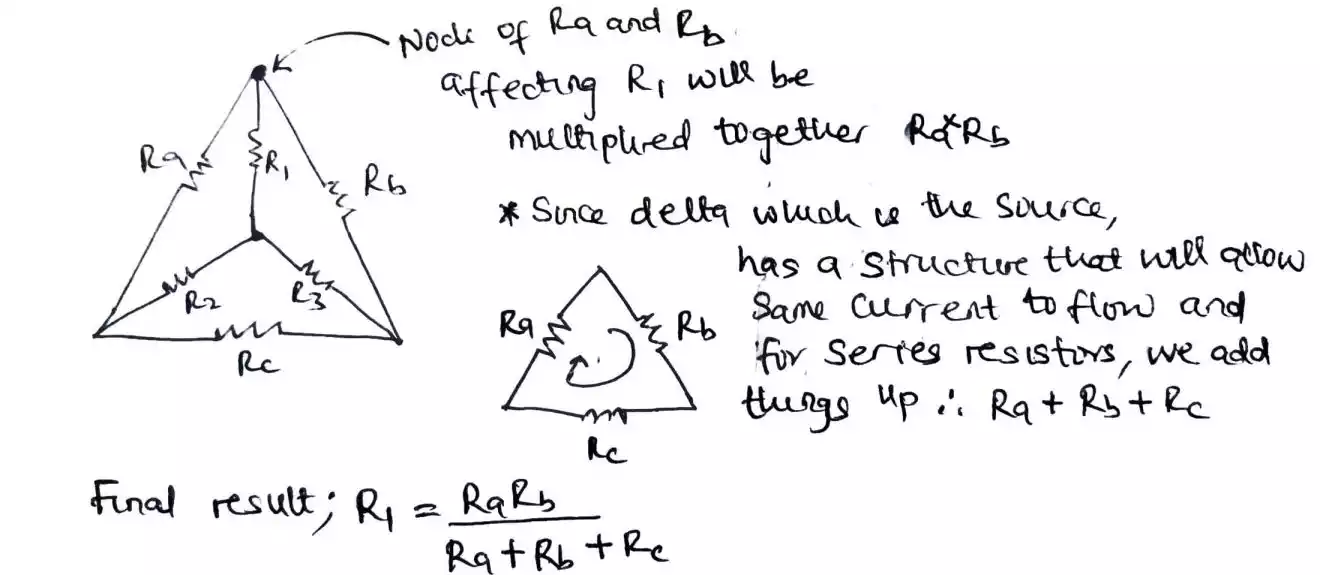
Then, since the delta is our source of conversion and also are connected in series (remember in series connected resistors, the values are added and the same current flows through them) therefore, we sum up (R_a + R_b + R_c) and then divide it by our first result which is R_a and R_b (remember we need to multiply R_a and R_b since they are affecting R₁).

Thus the transformation yields R₁ = (R_aR_b) / (R_a + R_b + R_c).

Doing same for R₂, we get R₂ = (R_aR_c) / (R_a + R_b + R_c) and for R₃ what will it be by doing it yourself without looking at the answer.

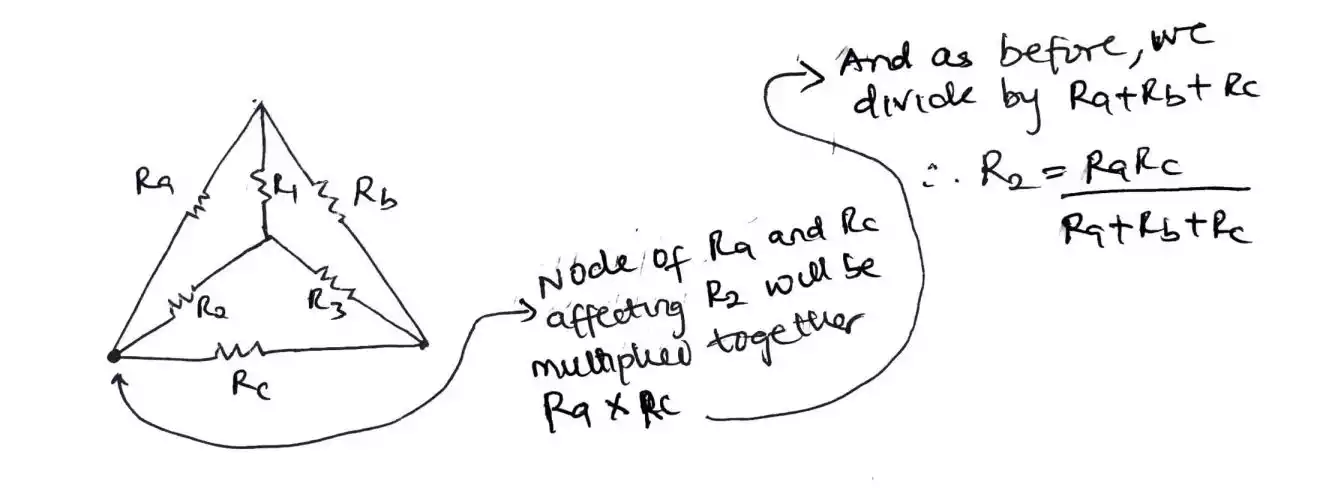
If you got the answer right, that’s good and in essence you can see, it's only the leg tied to our resistor in focus that matters since the bottom part (R_a + R_b + R_c) is same for R₁, R₂ and R₃.

The transformation or conversion from star to delta

Firstly, in this transformation, we are to find R_a, R_b and R_c as oppose to the last section where we are to find R₁, R₂ and R₃.

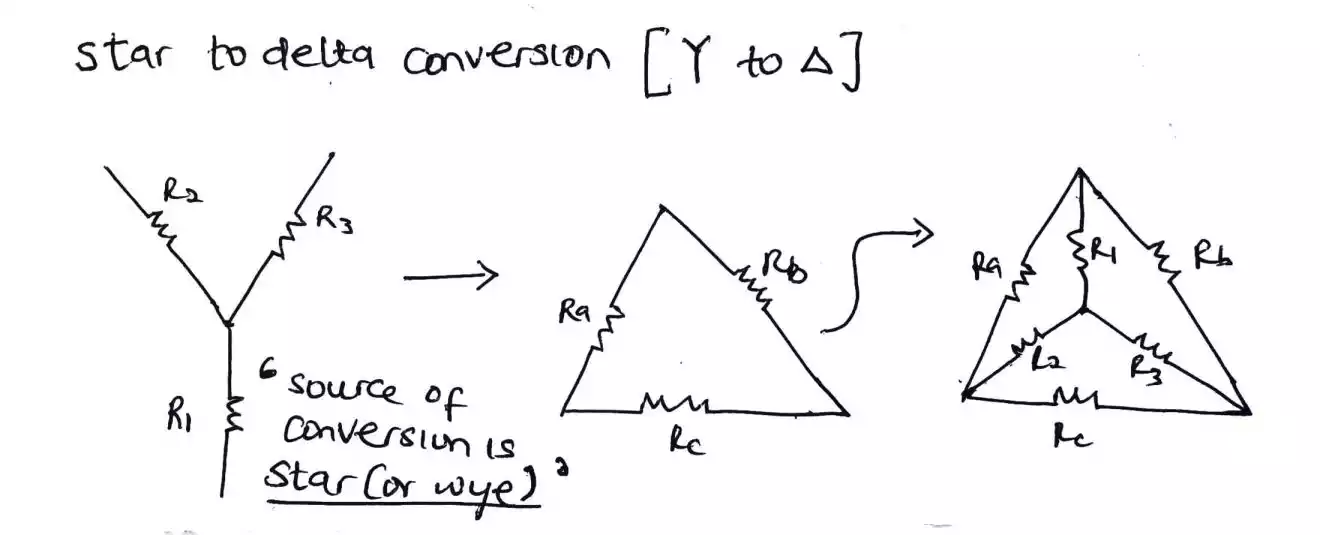
The formula is stated as

R_a = (R₁R₂ + R₂R₃ + R₃R₁) / R₃, R_b = (R₁R₂ + R₂R₃ + R₃R₁) / R₂ and R_c = (R₁R₂ + R₂R₃ + R₃R₁) / R₁

The formula for star to delta conversion

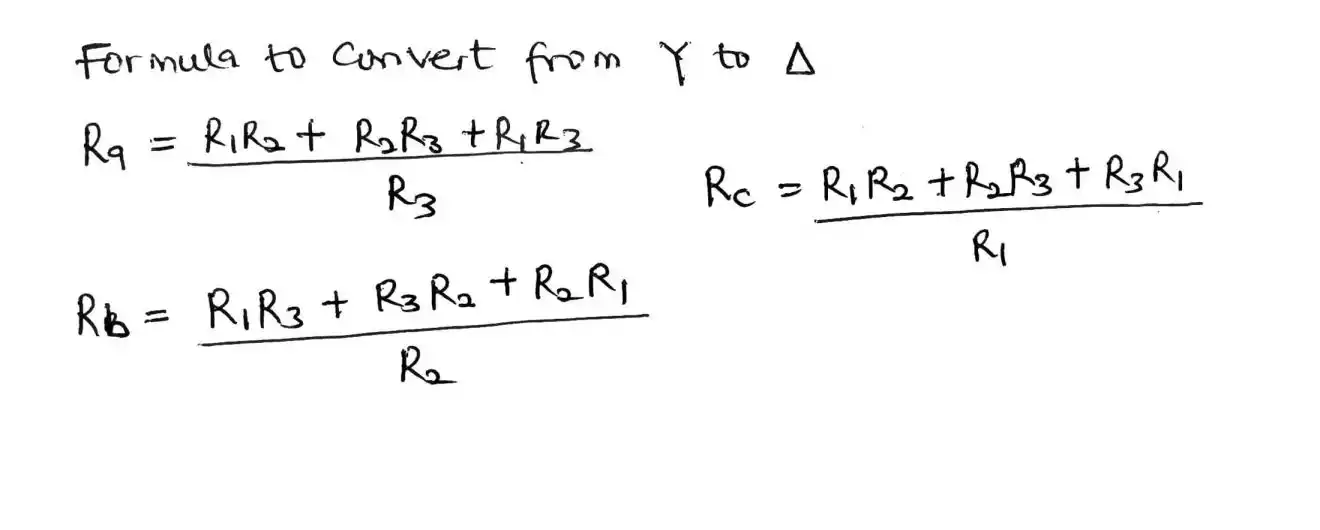
How to remember the formula for star to delta conversion

Now let’s recall the formula using our tip. First of all, you can see that R_a is affected by R₁ and R₂. And this R₁ and R₂ are also joined at a middle point to each other with R₃ so in that case we can’t just apply same rule as the previous one we did for converting from delta to star.

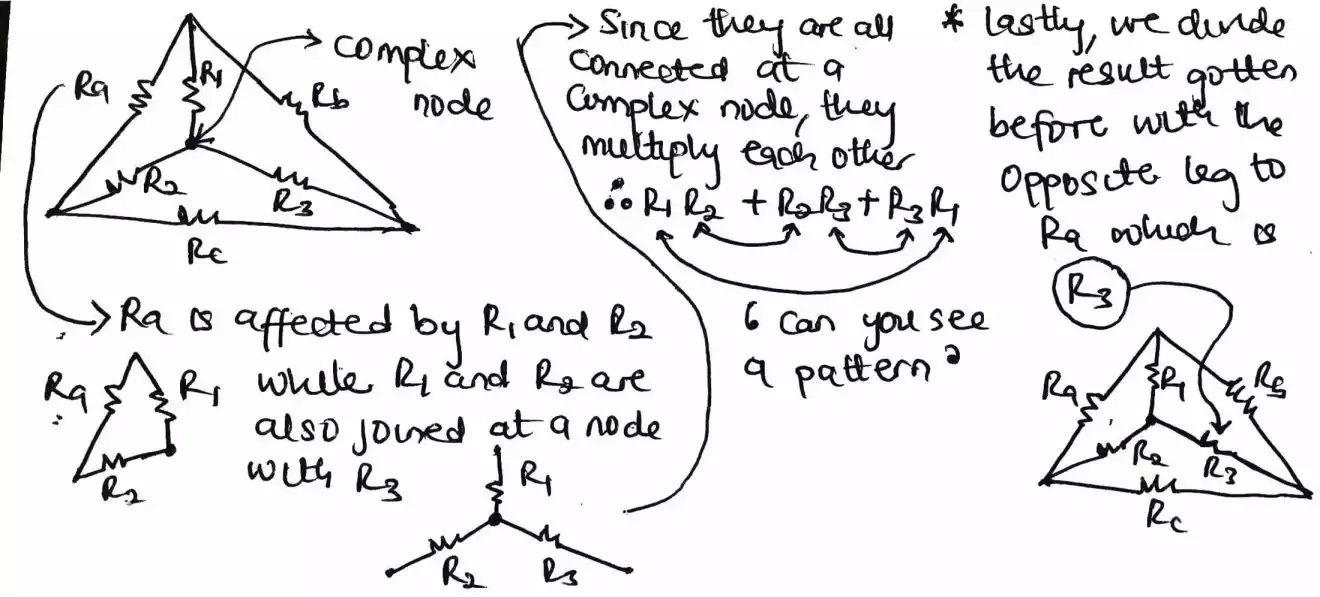
But what we need to do is, since R₁ and R₂ are tied to R_a and also R₁ and R₂ are connected at a node with R₃ then we just multiply R₁R₂ and then add R₂R₃ and lastly add R₃R₁ which yields this.

This step might look confusing a little bit but just go through it once more until you get the heck of it.

Tip

If you look at the previous two images, you will find where a pattern is shown - this can help in recalling the formula also.

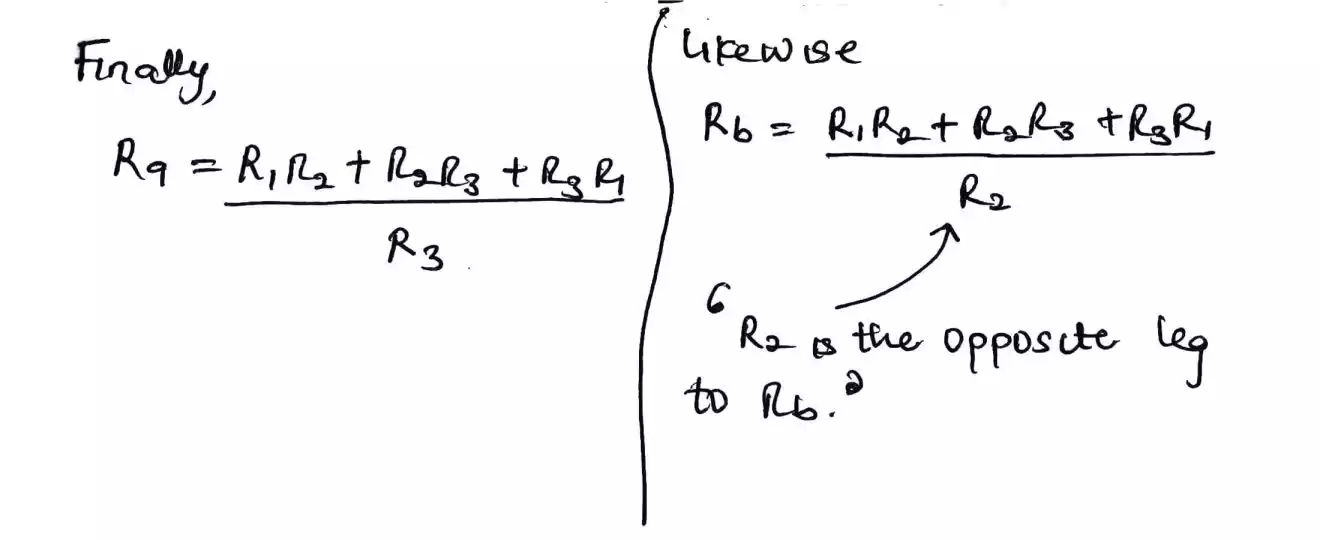
Then after that we divide our first result which is (R₁R₂ + R₂R₃ + R₃R₁) by the leg opposite to our R_a which is R₃ or we can say the leg not connected directly to R_a.

Likewise, R_b = (R₁R₂ + R₂R₃ + R₃R₁) / R₂.

Note

Since the top side is equal for all case and only the bottom changes, recall the bottom as the leg opposite to the resistor we are looking for. And in this case R_b and the leg opposite is R₂.

Now it’s your turn to do R_c and later check your answer.

Finally, let's try to recap all what we've just discussed by solving some examples.

Example on delta to star conversion

Ex.1 convert the delta network below to it star equivalent.

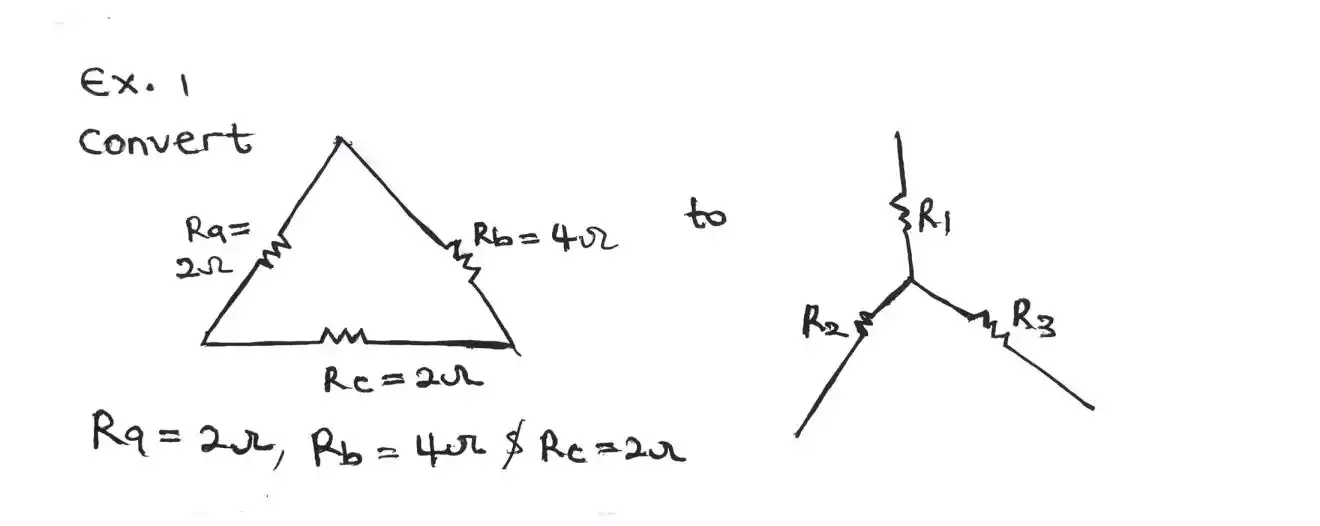
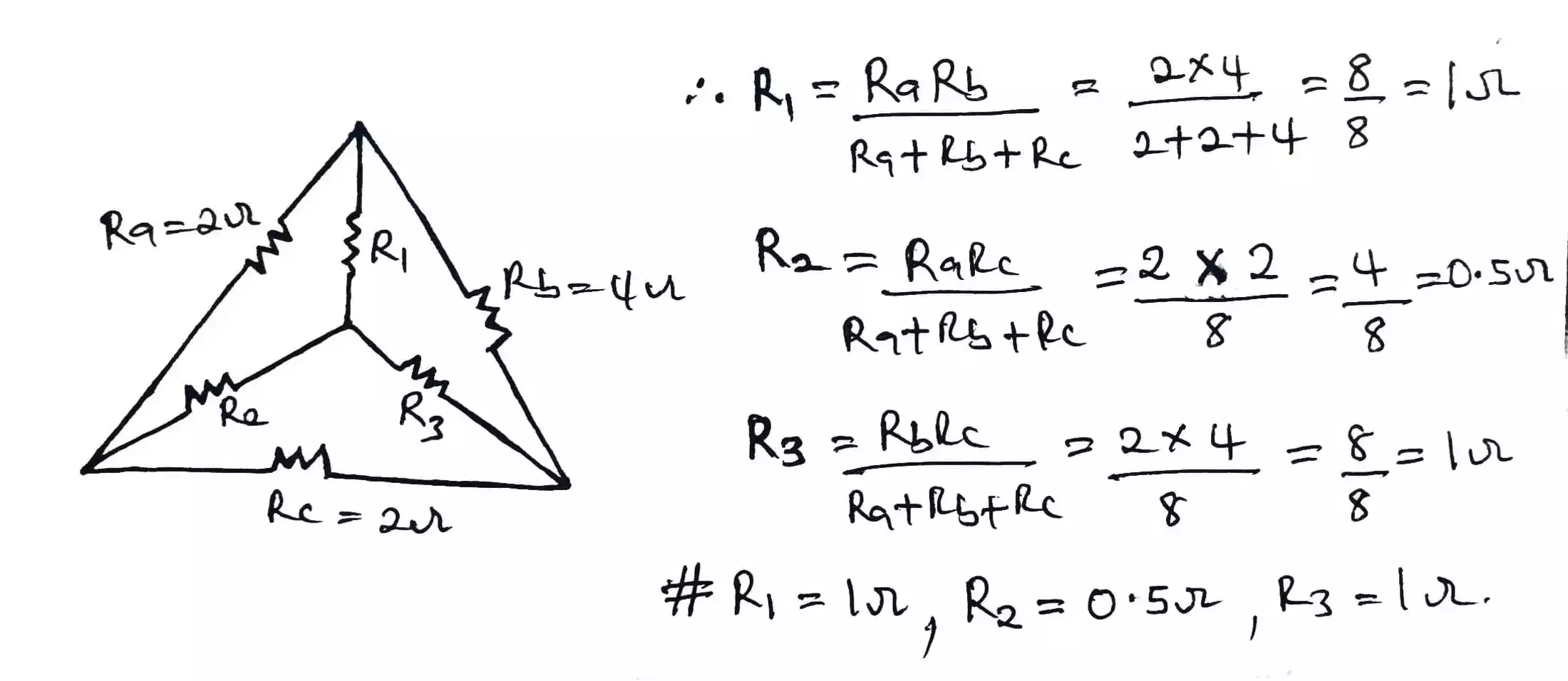
Firstly, we need to put the star network into the delta network and apply the corresponding formula

Example on star to delta conversion

Ex.2 let’s convert the star network gotten from Ex.1 back to the delta equivalent.

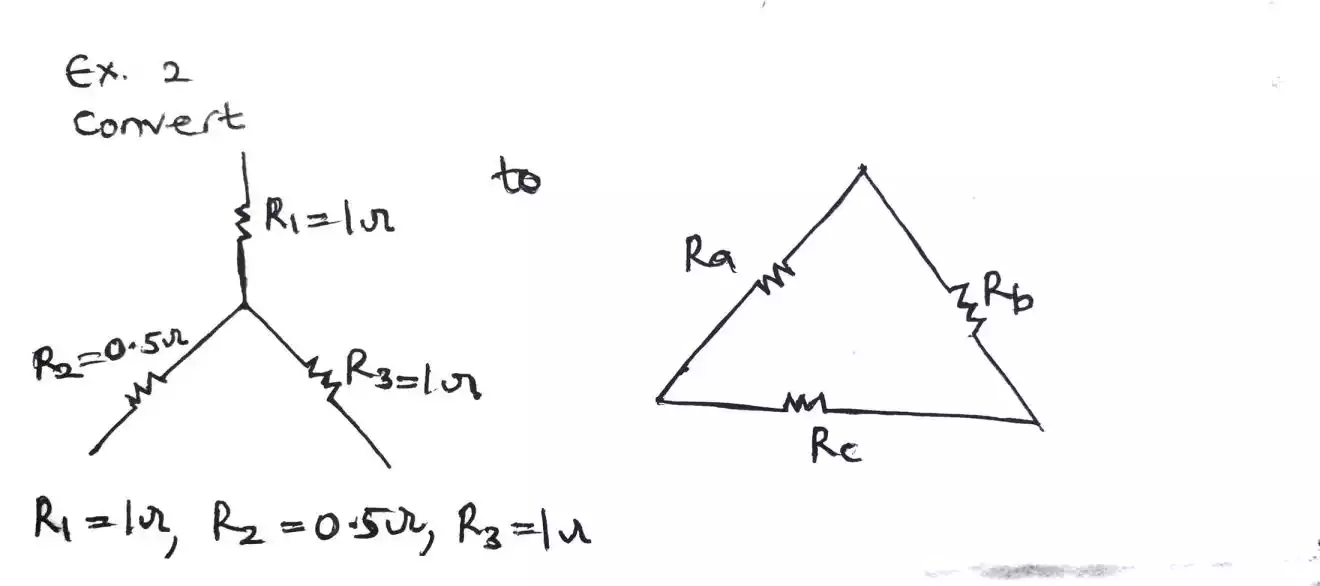
As always, we need to put the star network into the delta network and apply the corresponding formula

Here comes the end on this section and now it's your turn to tell us if this article does help or there is any feedback you need to give. Cheers tooabstracter. 🎉