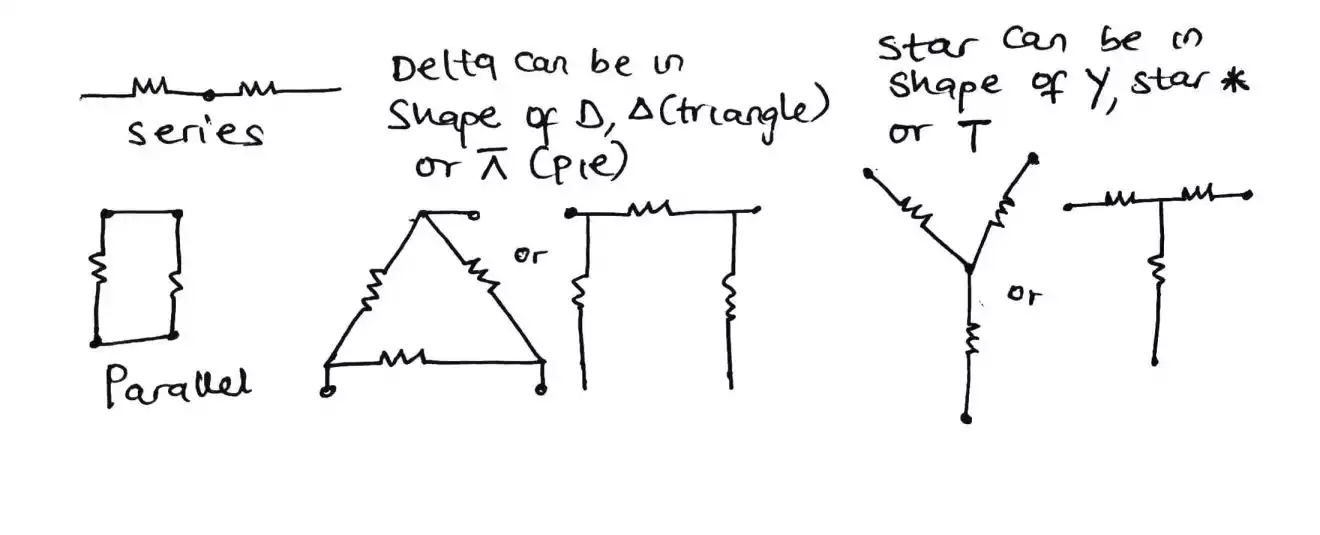
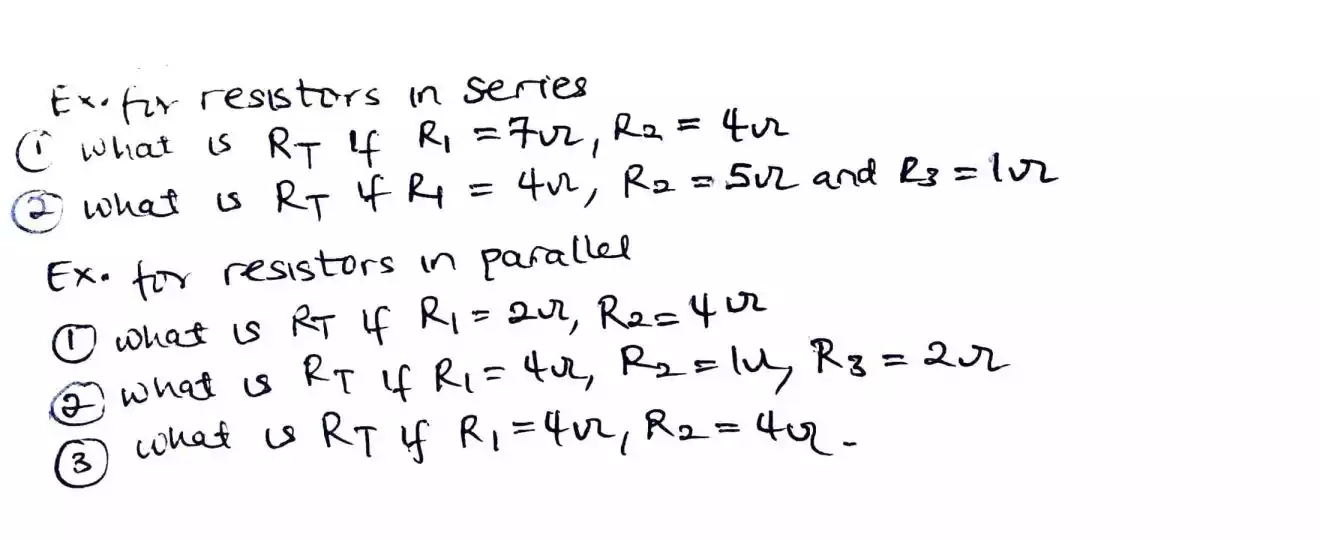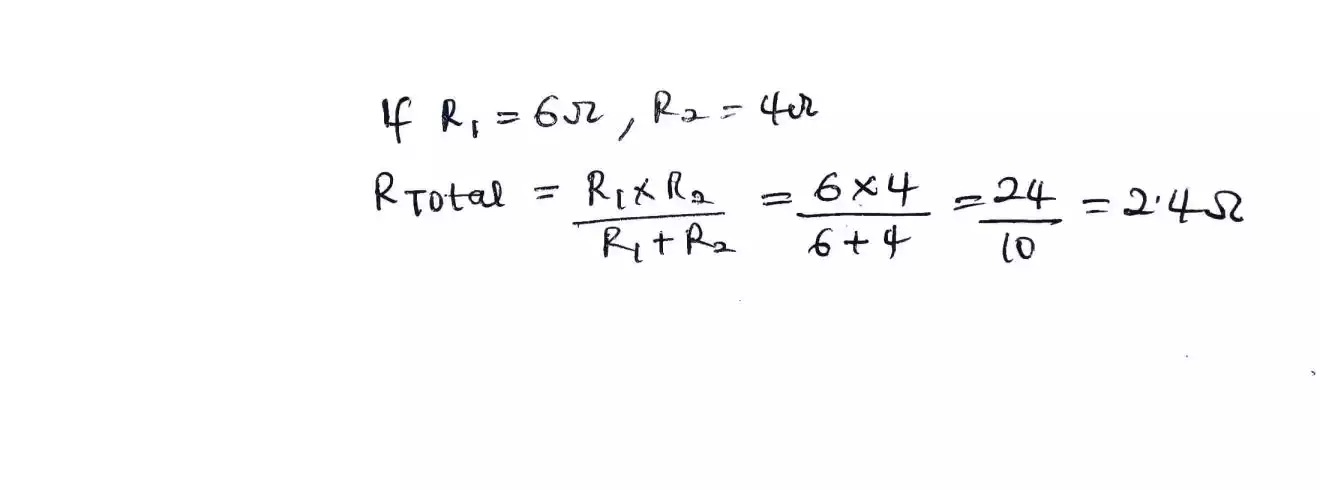Series and parallel connection of resistors
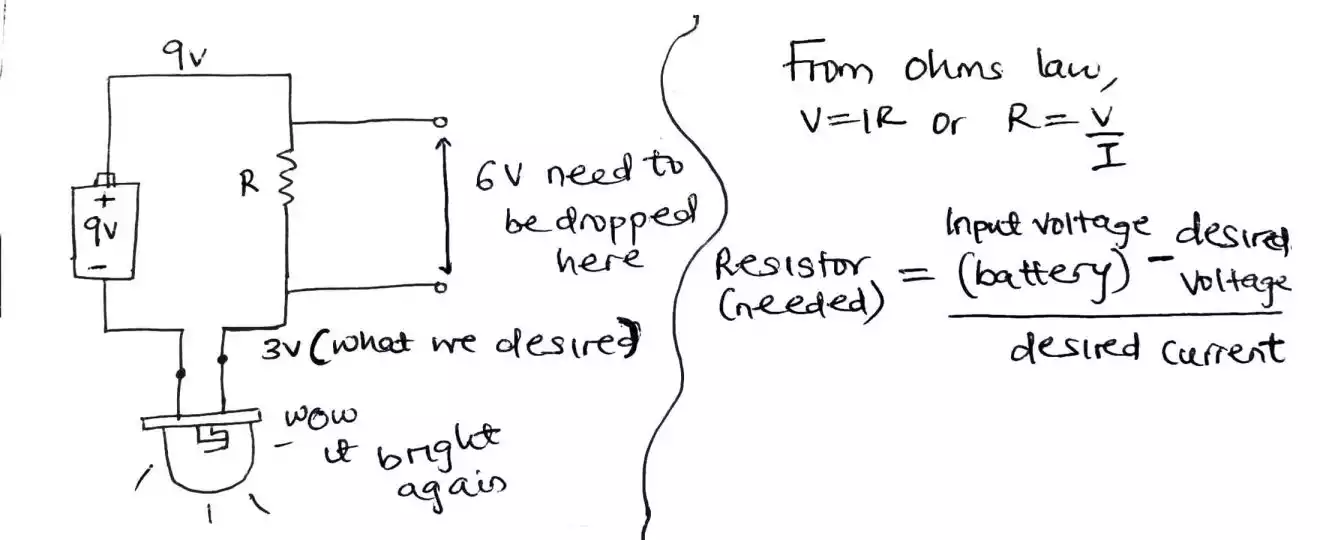
In the case whereby your bulb (or L.E.D) requires 3v to work but the only value of voltage at hand is 9v then, we need a resistor to reduce the current as well as cause a voltage to drop across the resistor so that the value of voltage at the output leg of the resistor will be 3v exactly or approximately.
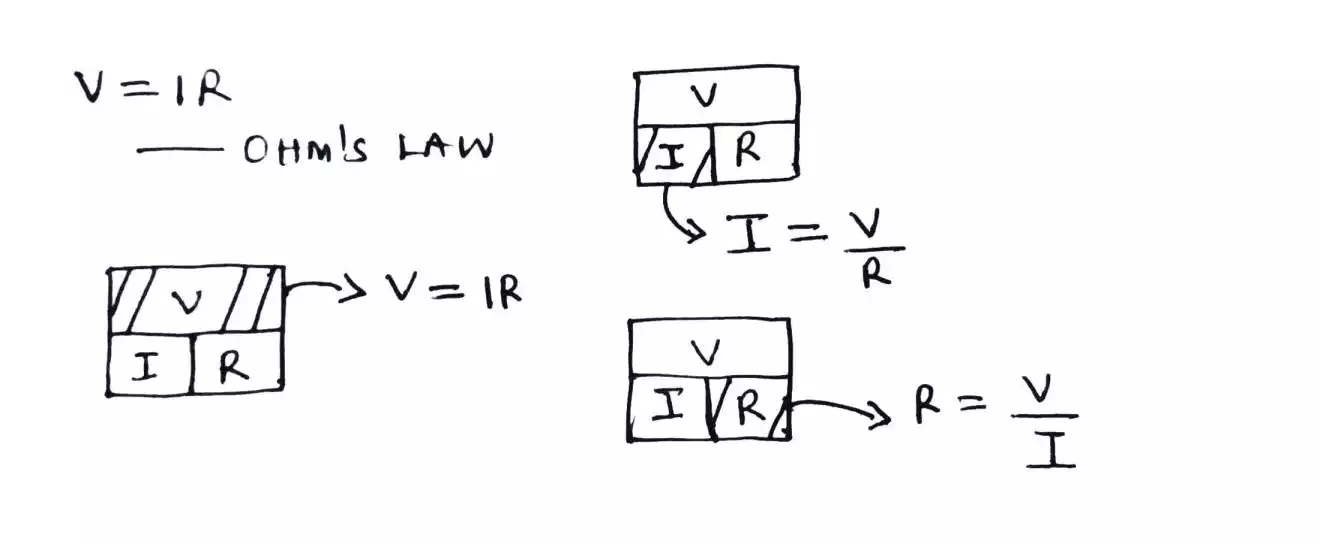
The way to find the resistance value of the resistor is by using the formula shown above.
Since our input battery is 9v and our desired voltage is 3v, we are to subtract 3v from 9v which gives us 6v then we divide by the amount of current we want to pass through our bulb (mostly it is 50㎃) then R will be 120Ω.
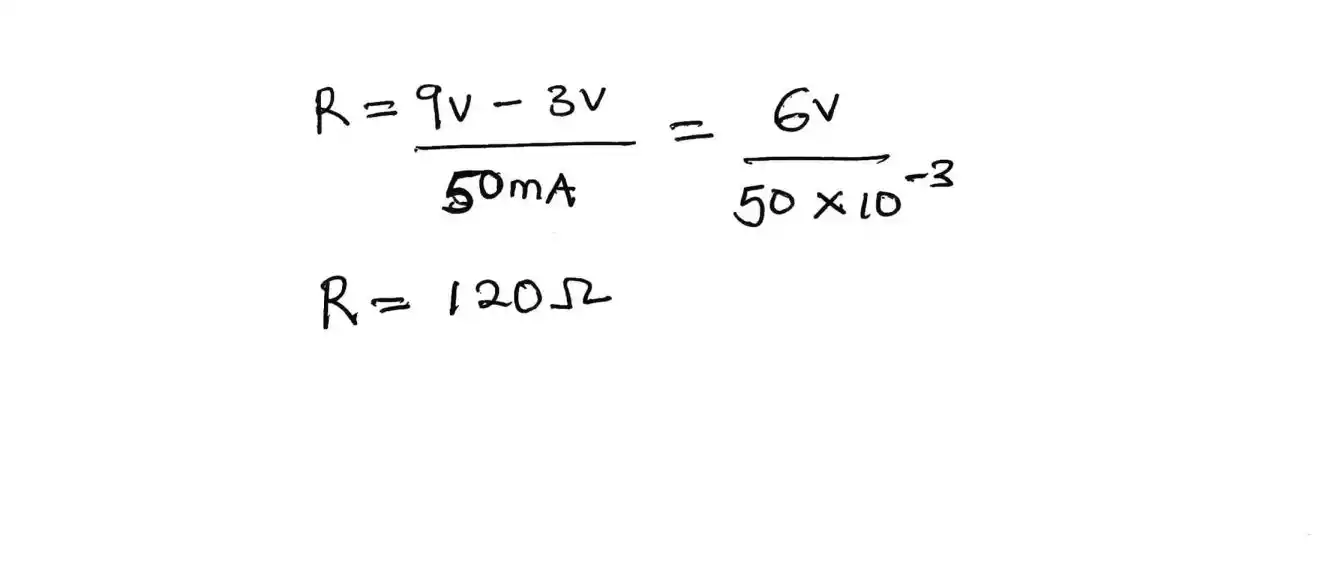
Now there is a problem still since if we go to the market to buy a resistor with a resistance value of 120Ω, there is no possibility of getting it rather we might get a 47Ω and 73Ω resistor which means we need to add these resistors up to get a total of 120Ω.
To do that is by joining them together tail to head (which we call series connection). As shown below
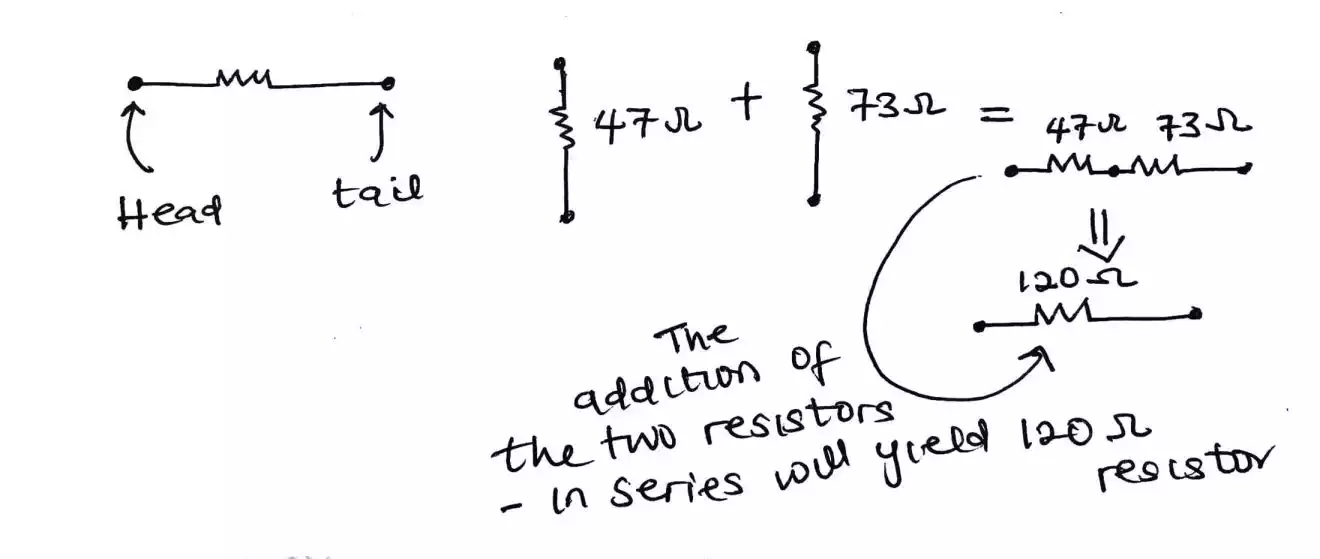
Which means if resistors are joined together in series then the equivalent or total resistance value of the resistors will be the sum of the resistors resistance value. if that sound complex, read it again because, resistors as we said in previous articles has a resistance value that tells the rate at which current will be reduced.
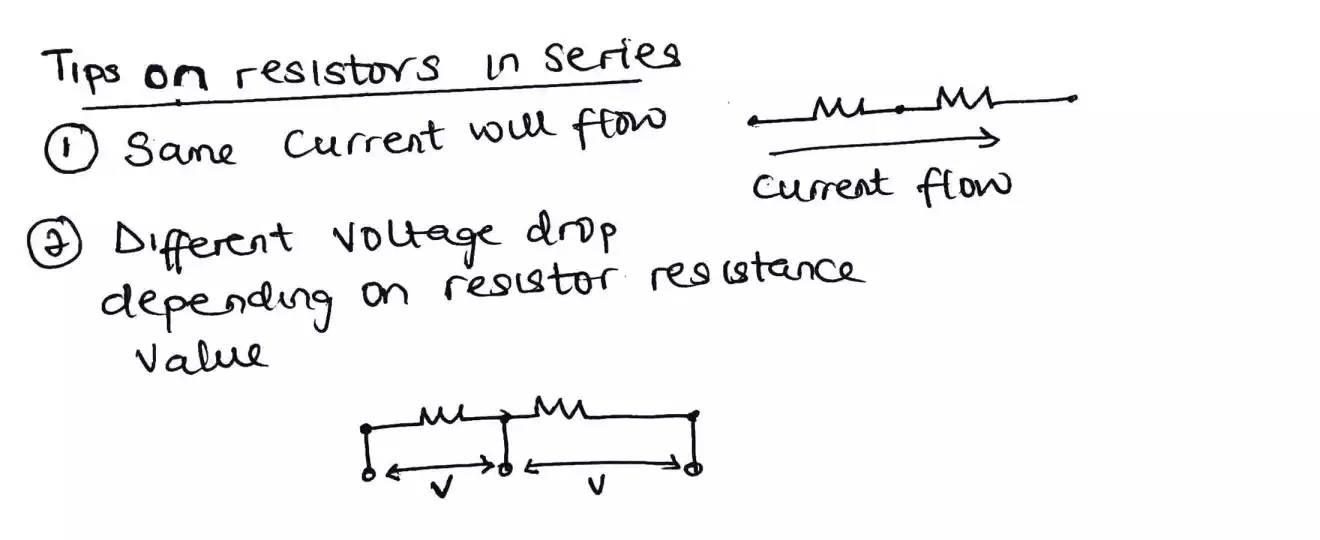
Resistors in series (allows us to add resistors)
A resistor in series allows the same current to flow through them but different voltage will be dropped across them if their resistance value is different.
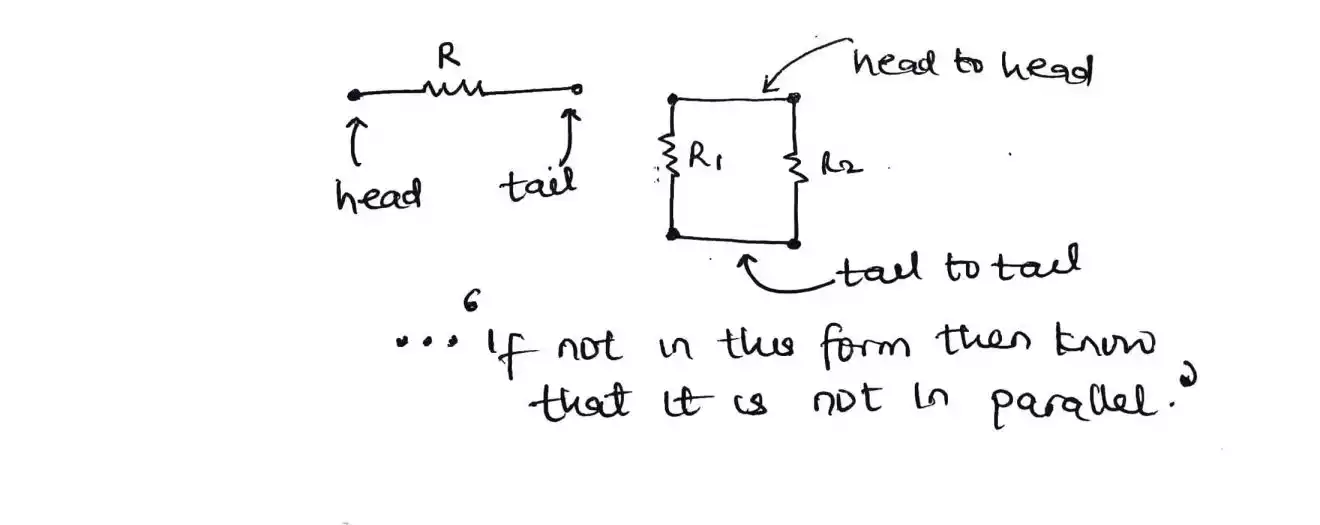
Resistors in parallel
As resistors are added up by joining them in series, the parallel is a little bit different since we join it head to head and tail to tail which means any resistor that are not in the form of series or parallel, it is considered to be in star or delta which we would be discussing later but for now let’s focus on resistors connected in parallel.
Here’s how resistors are connected in parallel as oppose to series
Resistors in parallel has two formulas which are shown below.

Two (2) resistors in parallel
Let’s do an example using two 10Ω resistor Ex.1: (R1 = 10Ω and R2 = 10Ω)

As you can see there is something fascinating that has just happened which means if we are looking for a 5ohms resistor, we can just pick two 10Ω resistor and connect them in parallel //.
As you can also see, I just show two forward slash which is a shortcut for saying resistors are in parallel.
But this technique works if the resistor we have at hand has a resistance value equal to 2 multiplied by the resistor we desired. Because as in the above example, we have 10Ω which is 2 * 5Ω.
Still, R1 and R2 can be of different value as we would be seeing an example shortly but I just want to show you some tips.
What will the equivalent resistance value be if R1 = 6Ω and R2 = 4Ω, try this and see answer below.
What happens when resistors are connected in parallel
Note
In esssence, when two or more resistors are put in parallel, the total resistances value is reduce as oppose to if resistors are connected in series which yields an increase in a total resistance value.
3 resistors in parallel
We use the second formula which looks a little bit boring but there is still a way to cheat (not really a cheat but a tip) which is, we would still be using the product/sum formula for two resistors in the case of solving 3 or more resistors instead of using the 1/Req or total = 1/R1 + 1/R2 + 1/R3 formula.
But let’s solve some example using this boring formula first
Ex.3 if R1=2Ω, R2=2Ω, and R3 =2Ω

Now let’s use our product/sum formula but remember, it works for two resistors in parallel only so therefore, we are to split the 3 resistors in parallel into two and one resistors.
If we solve for the two first, we will get an equivalent resistance value and then we are to join it with the last one we left earlier and apply same formula again.
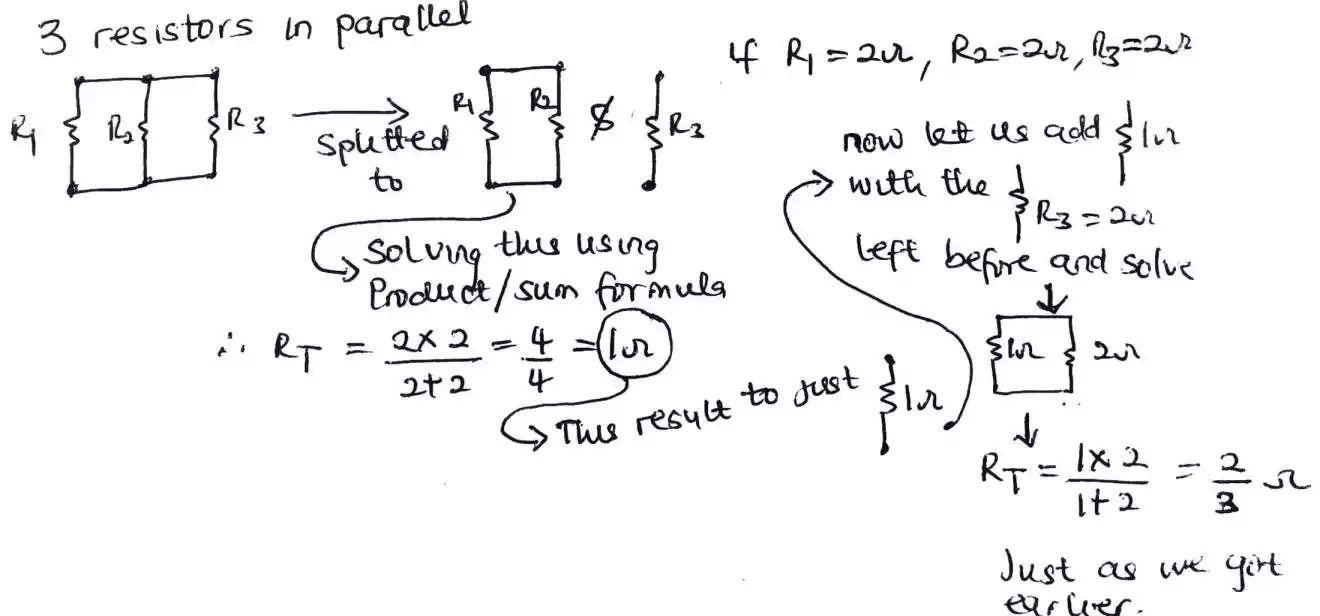
As you can see for the first two, we got a total resistance value of 1Ω
after then, we are to join this equivalent resistance value that we just got with the other 2Ω we left before so we are going to have a new total resistance value of 2/3Ω.
tip
A resistor in parallel have same voltage but different current will be flowing through each resistor depending on their resistance value.
Here are more examples you can try both on resistors in series and in parallel. Before moving to star and delta transformation.