Differences Between Causal and Non-Causal Signal
A signal can be defined as any physical quantity that carries information and varies with time, space, density, and other independent variable(s). It can also be defined as a pattern of variation in a physical quantity, such as sound or light, that can be measured and analyzed.
Signals can be classified into different categories or types based on various properties, such as the direction of the signal flow or the time-domain characteristics of the signal.
Causal and non-causal signals are among the types of signals that we have in electronics and Communications.
What is a Causal Signal?
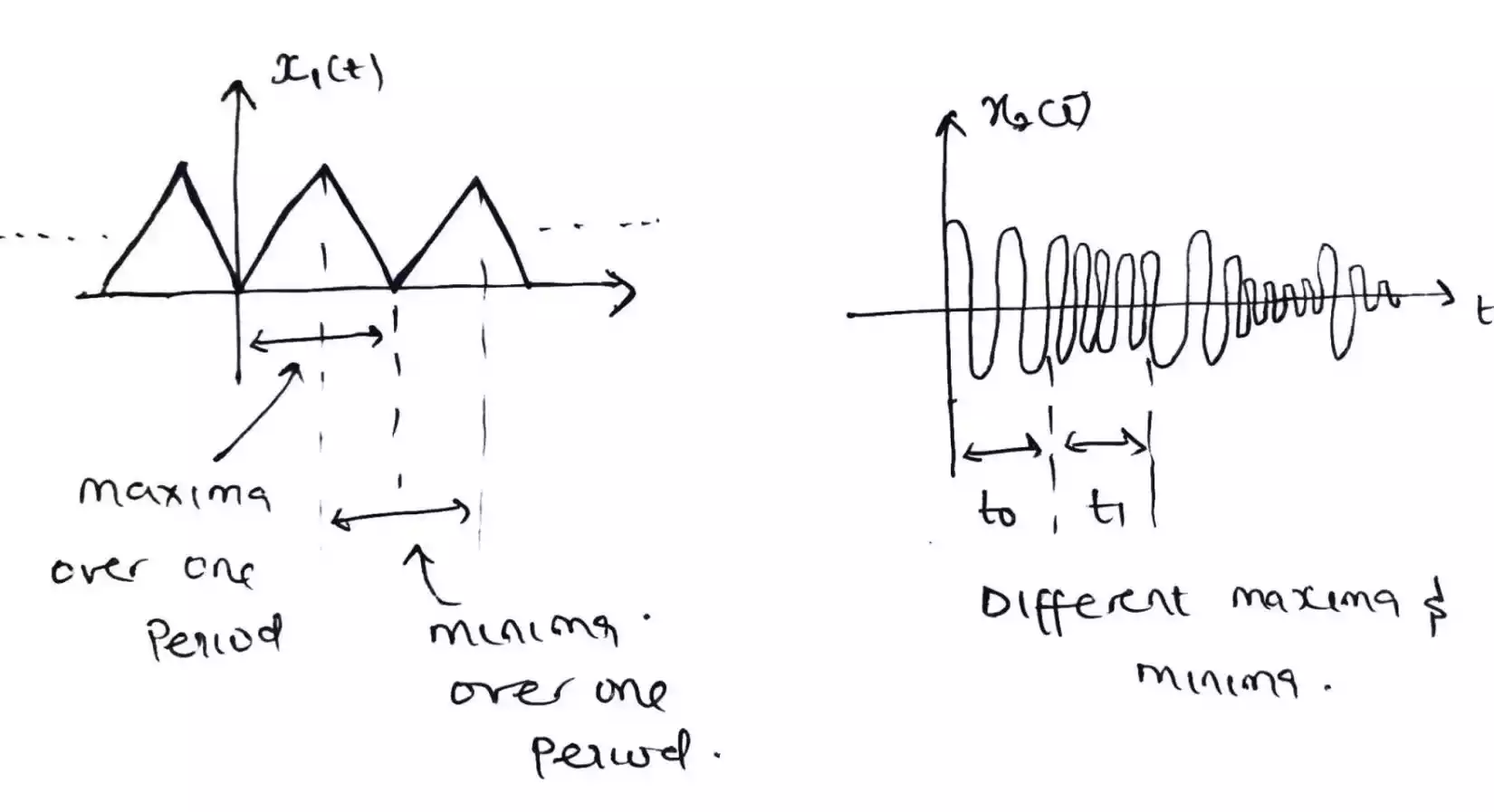
A causal signal is a type of signal that only depends on past or present values of time.
In other words, a causal signal can be predicted or can only exist by looking only at what has happened before or at the current time, without needing to know anything about the future.
Examples of causal signals include the temperature of a room, the sound of a clap, or the voltage across a resistor.
What is a Non-causal Signal?
A non-causal signal is a type of signal that depends not only on the past and present values of time, but also on the future.
In other words, a non-causal signal cannot be predicted by looking only at past and present values of time, but requires knowledge of future values as well.
Examples of non-causal signals include a prediction of tomorrow’s weather based on today’s temperature, or a signal that anticipates a sudden change in the stock market.
Differences between Causal and Non-causal Signals
#/ Causal Signal
- Causal signals depend only on past and present values of time.
- Causal signals can be processed using a wide range of signal processing techniques, such as filtering, convolution, and Fourier analysis.
- Causal signals are physically realizable, since they only depend on past and present values of time that can be measured and recorded.
- x(t) = e^(-at) * sin(ωt) is a damped sine wave and an example of a causal signal as it only depends on past and present values of time, and will eventually decay to zero as time goes to infinity. In this equation, a is a damping factor, ω is the frequency of the sine wave, and t is time.
- x(t) = u(t) is a step function, and it is an example of causal signal also, as it turns on at t=0 and remains constant thereafter. The function u(t) is the unit step function, which is defined as u(t)=0 for t < 0 and u(t) = 1 for t >= 0.
- Causal signal is a signal that has zero value for all negative time.
#/ Non-causal Signal
- Non-causal signals depend on past, present, and future values of time.
- Non-causal signals require more advanced signal processing techniques that can account for future values of time, such as time-reversal methods or prediction algorithms.
- Non-causal signals, however, are not physically realizable, as they require knowledge of future events that cannot be measured or recorded in advance.
- x(t) = a + bt + ct^2 + dt^3 + et^4 + … is a signal that can be used to predict stock prices. This signal represents a polynomial function of time, where the coefficients a, b, c, d, e, etc. are determined by fitting the function to past stock prices. While this signal can be used to predict future stock prices, it is non-causal, since it depends on both past and future values of time.
- x(t) = sin(ωt) + sin(2ωt) + sin(3ωt) + … is a signal that can be used to predict the weather. This signal represents a sum of sine waves with different frequencies, which are determined by analyzing past weather data. While this signal can be used to predict future weather patterns, it is non-causal, since it depends on both past and future values of time.
- Non-causal signal has no zero values in both the positive and negative time.