How Do You Solve Energy and Power Signals Problem Step By Step With Tips and Shortcuts?
Before solving problems on energy and power signal, you need to understand what each of the signal means
What are power and energy signals?
A power signals are signals with finite power while energy signals are signals with finite energy.
How do you solve energy and power signals?
Here are the few things to remember in order to quickly identify if a signal is a power or an energy signal
1. If the amplitude or value of the signal $x(t)$ is zero at t → to ∞, then the signal is an energy signal
For example
$x(t) = e^{-9t}u(t)$ by looking at this signal $x(t)$ you can see that $e^{-9t}$ is the amplitude or height of the step function signal $u(t)$ hence if t tends → to either –∞ or +∞ then $e^{-9t}$ result to zero according to the fact that $e^{0}$ = 1 and $e^{∞}$ =0.
So as the amplitude of the signal is zero then you know it is an energy signal and then if you wish you can proceed to solving it using the energy signal formula thar will be discussed shortly.
Note:
An aperiodic or non-periodic signal is considered to be an energy signal because the area under the curve is finite
Example of a non-periodic or energy signals
- $Ae^{-at}u(t)$ e.g. $2e^{-at}u(t)$
where A can be any constant value.
2. If the amplitude or value of the signal is constant at t → to ∞ then the signal is a power signal For example
$x(t) = 4\sin(wt)$ is a power signal as the amplitude is constant and it is equal to (4).
.webp)
Note:
From this then you need to note that all periodic signals or functions are power signals since they all have constant amplitude.
Examples of periodic or power signals
- $A\sin(wt)$ e.g. $5\sin(2t)$
- $A\cos(wt)$ e.g. $3\cos(4t)$
- $A\tan(wt)$ e.g. $2\tan(7t)$
- $Ae^{jwt}$ e.g. $4e^{j4t}$
where A can be any constant value.
What signal is neither a power nor an energy signal.
A function or signal that is neither a power or energy signal is a ramp function and it is because when you calculate for the energy and power signal, in both cases they are infinity.
$r(t)$ = $tu(t)$, E = ∞ and P = ∞
Also a function like this one below has an energy and a power equal to zero hence, can also be considered neither an energy or power signal.
$x(t)$ = $e^{-at}$, E = 0; and P = 0;
That’s the first step to know if a signal is either a power or an energy signal. But what if you can’t easily tell and also you are asked to solve the signal and verify if it is a power or energy signal using it formula.
First here is a table below that tells if a signal is a power or an energy signal.
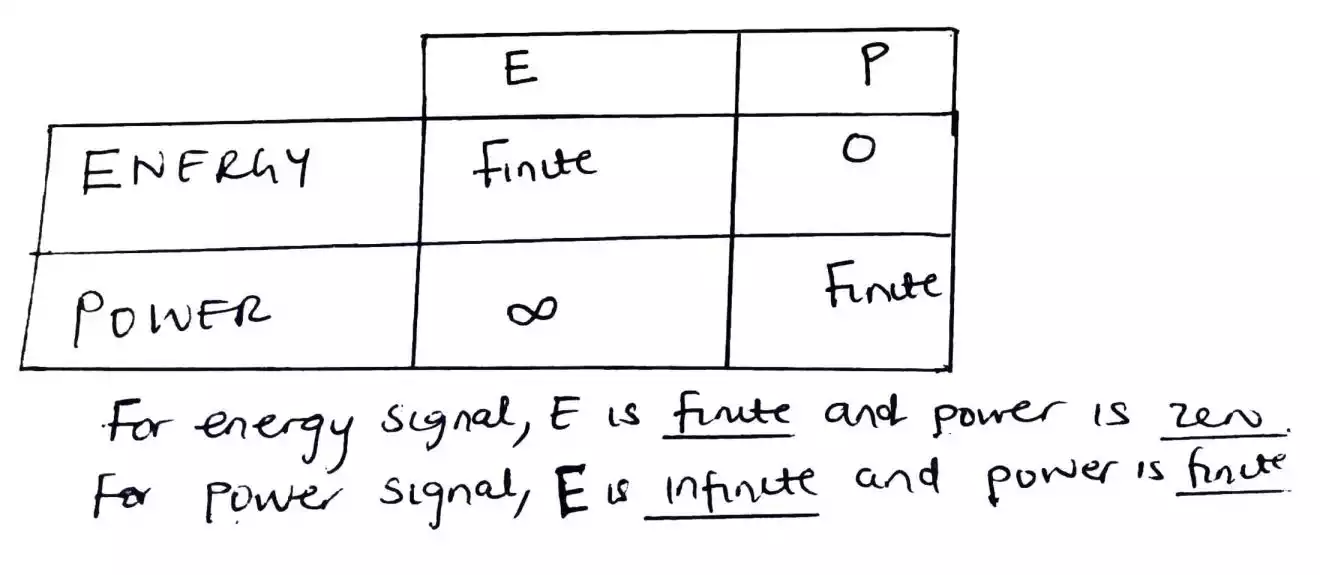
As you can see when a signal is an energy signal, it will have a finite energy and a zero average power. But when the signal is a power signal, it will have a finite power but an infinite energy.
Formula for energy signal and power signal
$$E =\lim_{T \rightarrow ∞ } = \int_{-T}^{T} |x(t)|^{2} dt$$
or
$$E = \int_{-∞}^{∞} |x(t)|^{2} dt$$
$$P = \lim_{ T\rightarrow ∞}\frac{1}{2T} \int_{-T}^{T} |x(t)|^{2} dt$$
Steps to follow are;
- If you are given a function $x(t)$
- Find the modulus or absolute value of the signal $|x(t)|$
- Find the integral of the square of the modulus of the signal $\int_{-T}^{T} |x(t)|^{2} dt$
- Take the limit as it tends to infinity of the above integral to find what the energy is $E =\lim_{T \rightarrow ∞ } = \int_{-T}^{T} |x(t)|^{2} dt=$
- Then proceed to finding what the power is by dividing the energy by the total period - as power is energy over time. $P = \lim_{ T\rightarrow ∞}\frac{1}{2T} \int_{-T}^{T} |x(t)|^{2} dt$
Energy and power signals - solved examples
Find whether the following signals are energy signals or power signals or neither of them.
-
$x(t) = e^{-at}u(t), -∞ < t < ∞$
$|x(t)| = e^{-at}u(t)$
$\int_{-T}^{T} |x(t)|^{2} dt = \int_{-T}^{T} |e^{-at}u(t)|^{2}dt$
$\int_{-T}^{T} e^{-2at}(u(t))^{2}dt$
Since $u(t)$ is a unit step function with amplitude (or value) of 1 then it square will also be 1
$\therefore (u(t))^{2} = u(t)$ hence,
$\int_{-T}^{T} e^{-2at}u(t)dt$
But also $u(t)$ is always defined for $t>0$
$\therefore$ The limit changes from $\int_{-T}^{T}$ to $\int_{0}^{T}$ and then $u(t)$ will be eliminated
hence, $\int_{0}^{T} e^{-2at}dt$
Now taking the integral and substituting, we have $\frac{e^{-2at}}{-2a}\mid_{0}^{T}$
$\frac{e^{-2at}}{-2a}\mid_{0}^{T}$ = $\frac{e^{-2aT}}{-2a}$ - $\frac{e^{-2a(0)}}{-2a}$
Since $E =\lim_{T \rightarrow ∞ }\int_{-T}^{T} |x(t)|^{2} dt$
then $E =\lim_{T \rightarrow ∞ } (\frac{e^{-2aT}}{-2a} - \frac{e^{-2a(0)}}{-2a})$ =
$(\frac{e^{-2aT}}{-2a} + \frac{1}{2a})$ as $e^{-2a(0)}$ = 1;
Also by substituting ∞ in T,
$(0 + \frac{1}{2a})$ as $e^{-2a(∞)}$ = 0;
Hence, $E = \frac{1}{2a}$ which has a finite value only at $a > 0$
So if a = 2, $E = \frac{1}{2\ x\ 2}$ , $E = \frac{1}{4}$.
To further verify, we have to calculate for the power by just putting $\frac{1}{2T}$
$P =\lim_{T \rightarrow ∞ } \frac{1}{2T}(\frac{e^{-2aT}}{-2a} - \frac{e^{-2a(0)}}{-2a})$
$P =\lim_{T \rightarrow ∞ } \frac{1}{2T}(0 + \frac{1}{2a})$ = 0; as $\frac{\frac{1}{2a}}{∞}$ = 0.
So the function $x(t) = e^{-at}u(t), -∞ < t < ∞$ is an Energy Signal.
-
$x(t) = 4\sin(2\pi t), -∞ < t < ∞$
$|x(t)| = 4\sin(2\pi t)$
$\int_{-T}^{T} |x(t)|^{2} dt = $
$\int_{-T}^{T} |4\sin(2\pi t)|^{2}dt$
$16\int_{-T}^{T} \sin^{2}(2\pi t)dt$
But $sin^{2}(\theta)$ = $\frac{1 - \cos2\theta}{2}$ where $\theta$ from the example is $2\pi t$
So $16\int_{-T}^{T} \frac{1 - \cos2\ (2 \pi t)}{2}dt$ =
$16\int_{-T}^{T} \frac{1 - \cos\ (4 \pi t)}{2}dt$
$\frac{16}{2}\int_{-T}^{T} {1 - \cos(4 \pi t)} dt$ =
$8[\int_{-T}^{T} {1} dt - \int_{-T}^{T} {\cos(4 \pi t)} dt]$ =
$8[t - \frac{\sin(4 \pi t)}{4 \pi}] \mid_{-T}^{T}$ =
$E = lim_{T \rightarrow ∞ } 8[t - \frac{\sin(4 \pi t)}{4 \pi}] \mid_{-T}^{T}$ =
Note: The limit of $\sin$ or $\cos$ → to ∞ is zero so $\frac{\sin(4 \pi t)}{4 \pi}$ also will be zero.
So our function is now simpler,
$E = lim_{T \rightarrow ∞ } 8[t] \mid_{-T}^{T}$ = $E = lim_{T \rightarrow ∞ } 8[T - (-T)]$ =
$E = lim_{T \rightarrow ∞ } 8[T + T]$ = $E = lim_{T \rightarrow ∞ } 8[2T]$ =
$E = lim_{T \rightarrow ∞ } 16T$ = ∞
And now verifying for the power, $P = lim_{T \rightarrow ∞ } \frac{1}{2T}(16T)$ =
$P = lim_{T \rightarrow ∞ } 8$ = 8;
So as Energy is ∞ and Power is Finite (i.e. 8) then the signal is a power signal.
-
$x(t) = tu(t), -\infty < t < \infty$
$| x(t)| = |tu(t)| = tu(t)$
$| x(t)|^2 = |tu(t)|^2 =$$ t^2(u(t))^2 = t^2u(t)$, Since $u(t)$ has a value of one so if you square it it will still be one.
$\int_{-T}^{T} | x(t)|^2 dt =$
$\int_{-T}^{T} t^2u(t) dt$
$\int_{0}^{T} t^2dt = \frac{t^3}{3}|_{0}^{T}$
$= \frac{T^3}{3} - 0$
$\therefore \int_{-T}^{T} | x(t)|^2 dt =$
$\frac{T^3}{3}$
$E = \lim_{T \rightarrow \infty} \frac{T^3}{3} =$
$\frac{\infty^3}{3} = \infty$
$P = \lim_{T \rightarrow \infty} \frac{1}{2T} \frac{T^3}{3} =$
$\frac{T^2}{6} = \frac{\infty^2}{6} = \infty$
Since both Energy and Power are infinity, they are neither power nor energy signal.