Solved: Verify that the conduction current in the wire equals the displacement current ...
Question:
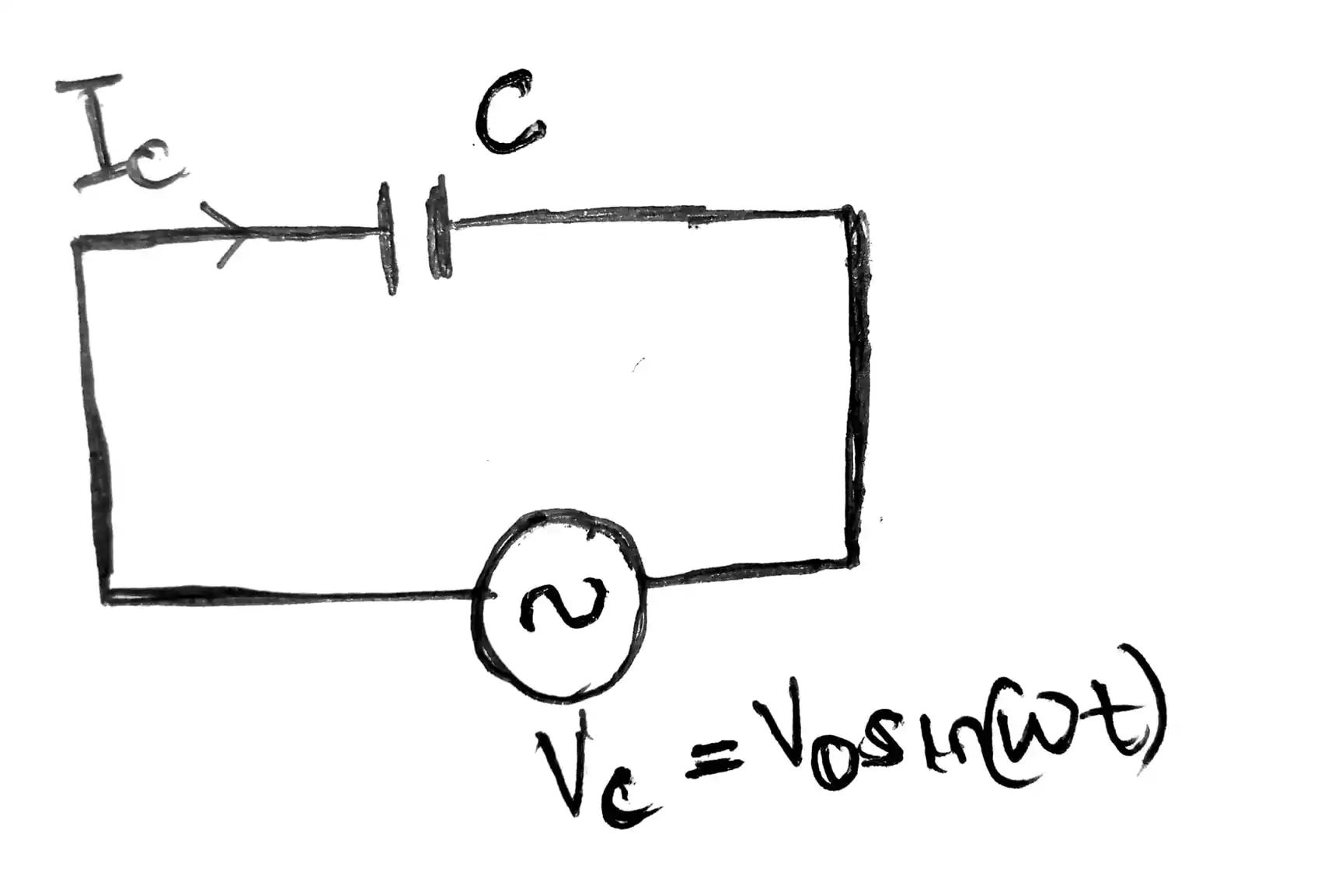
Verify that the conduction current in the wire equals the displacement current between the plates of the parallel plate capacitor in the figure below.
The voltage source supplies $V_c = V_o\sin\omega {t}$.
Solution:
The question is asking us to compare if the conduction current $I_c$ and the displacement current $I_d$ are equal.
Thus, we need to calculate for each.
1. Conduction current (Ic) = ?
From the circuit, we can see that, the current flowing in the circuit is the same as the current passing through the capacitor.
Hence, we can use $I_c = C\frac{\text{d}V_c}{\text{d}t}$.
Where:
$C$ is capacitance of the capacitor. $C =\frac{ \epsilon A}{d}$
$V_c$ is the voltage across the capacitor, which is the same as the input voltage source $V_c = V_o\sin\omega{t}$.
Therefore, $I_c = C\frac{d(V_o\sin\omega t)}{dt}$
If we differentiate the voltage, we have $I_c = C V_o \omega\cos\omega t$.
Now let’s find the displacement current $I_d$.
2. Displacement current $(I_d)$ = ?
But $I_d = \int\int J_d \cdot ds$ (surface integral of displacement current density over a surface)
This is also equal to the surface integral of $\int\int\frac{\partial D}{\partial t} \cdot ds$
Where:
$D$ (is electric flux density). It can also be expressed in terms of electric field intensity ($E$) as $D = \epsilon E$
Hence, $I_d = \int\int J_d \cdot ds = \int\int\frac{\partial D}{\partial t} \cdot ds$.
But $E$ can also be expressed in terms of $\frac{V }{D} \frac{(voltage [V])}{(distance [m])}$
Hence, $D = \epsilon\frac{V }{D} \frac{(voltage [V])}{(distance [m])}$
So to solve for $I_d = \int\int\frac{\partial D}{\partial t} \cdot ds$, we need to differentiate $D$.
Therefore, $I_d = \int\int\frac{\partial D}{\partial t} \cdot ds$.
$\frac{\partial D}{\partial t} = \frac{\epsilon\cdot V_o}{d} \omega\cos\omega t$
$I_d = \int\int(\frac{\epsilon\cdot V_o}{d} \omega\cos\omega t) \cdot ds $
$= \int\int ds (\frac{\epsilon\cdot V_o}{d} \omega\cos\omega t) $.
$\int\int ds$ = Area of the surface $(A)$
By substituting $A$, $I_d = A (\frac{\epsilon\cdot V_o}{d} \omega\cos\omega t)$
Remember that $C = \frac{\epsilon A}{d}$
Therefore, $I_d = C V_o\omega\cos\omega t$.
So in conclusion, by comparing $I_c$ and $I_d$, we can see that they are equal. i.e., $I_c = I_d = C V_o\omega\cos\omega t$.