What Is a Random Process With Examples?
Note: don’t fright out over the equation or formulas present in this article as we are to explain each bit by bit.
What is a random process?
A random process is also termed as a stochastic process and it is a process in which consist of several random variables over time. So you might ask what is a random variable?
A random variable is a variable with set of random numbers. Here is what I mean using an example.
Example of a random process and a random variable
Let us take the weather temperature throughout the day in New York as an example. As you can see the graph is showing how the weather changes through the day (or over a 24-hour time period).
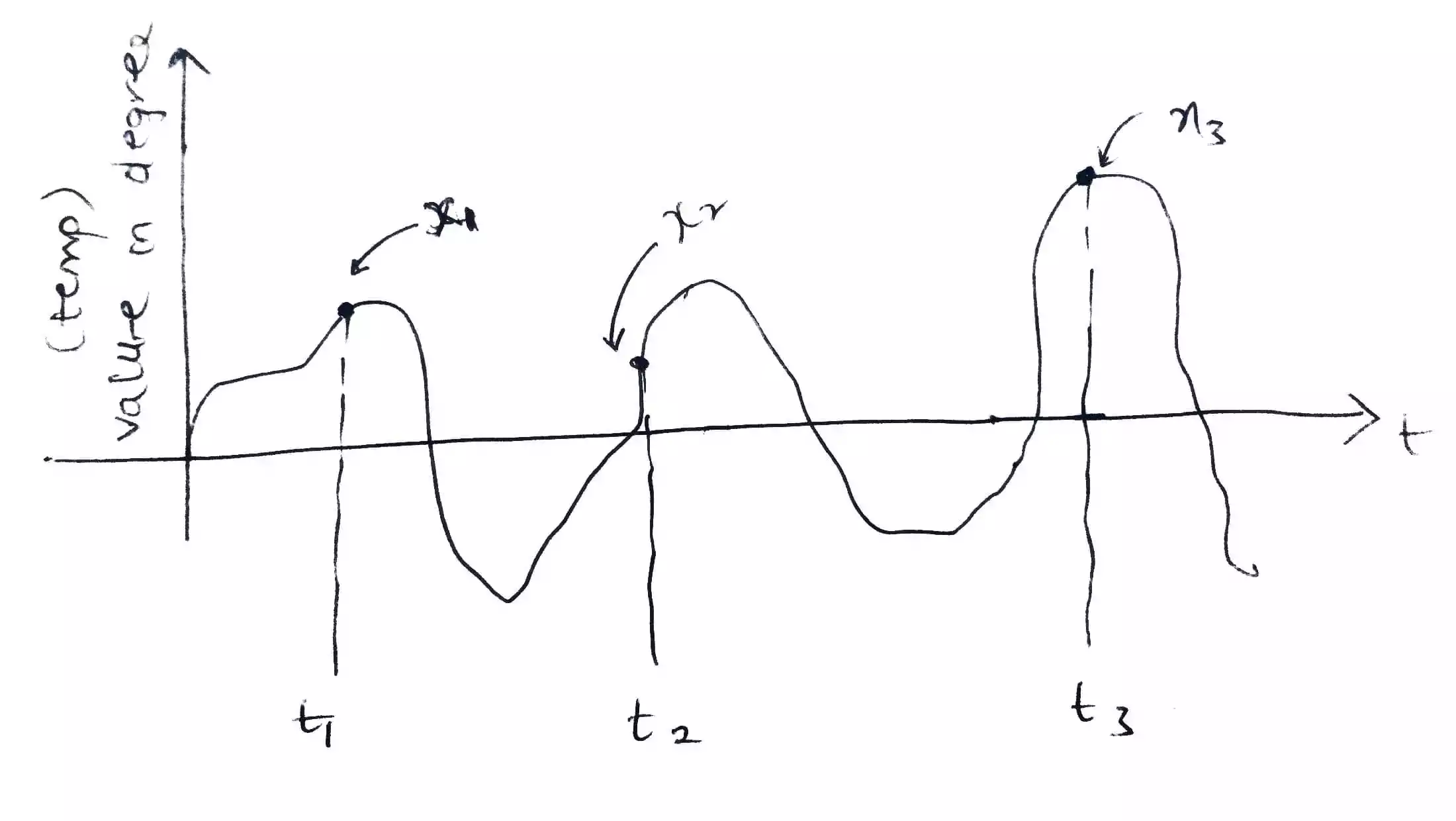
At t1 we assume it is 5am in the morning, t2 is 11am in the morning and t3 is 3pm in the afternoon.
Now at t1 we assume the value of the temperature in degree is x1 = 42o, at t2 the value is x2 = 47o and at t3 the value is x3 = 47o.
Those values in degree are the values we take at random time and we can combine them together into a variable called random variable.
This random variable as it changes with time then it is termed as random process.
In essence, random variable is associated with values and it is denoted as (capital x) X which contain (small x which are the values at random) and for our temperature example, we have 3 small x’s (x1, x2 and x3)
so therefore, X (random variable) = {x1, x2, x3}
Now for the random process, it is denoted as (capital X of t) X(t) since it is associated with time.
Therefore, X(t) = {x1(t), x2(t), x3(t)}.
Type of random processes
Strict sense stationary random process A random process is said to be strict sense stationary or simply stationary if none of its statistics is affected by a shift in time origin. i.e. the occurrence of a function x(t1) at t1 is same at x(t2) when there is a shift from 1 to 2.
Wide sense random process A random process is said to be wide sense stationary if two of its statistics (mean and autocorrelation) is not affected by a shift in time origin or do not vary with a shift in time.