Crammer's rule - the technique to simplify circuit analysis equations

Solving simultaneous equations containing more than two variables can be quite daunting if we use either elimination method or substitution method because, thing gets a little bit complex.

Also, crammer's rule has been a technique used by engineers, students and by professors due to it compactibility and conciseness and lastly you can choose to use a calculator to help you solve that very fast.

Now back to business, variable names can be x and y or a and b or Ia and Ib (as we do in circuit analysis for currents), it’s up to you to choose what you want.

The most important thing is to find a way to simplify or find a final solution to our problem through the set of equations gotten from our circuit problems.

Also to note is that solving simultaneous equation by elimination or substitution method is much more related to crammer’s rule and we would be looking at that later on but for now let’s focus on crammer’s rule.

The crammer's rule

Crammer's rule says if we have an equation with two unknowns or even more but for now let us deal with 2 unknowns as shown

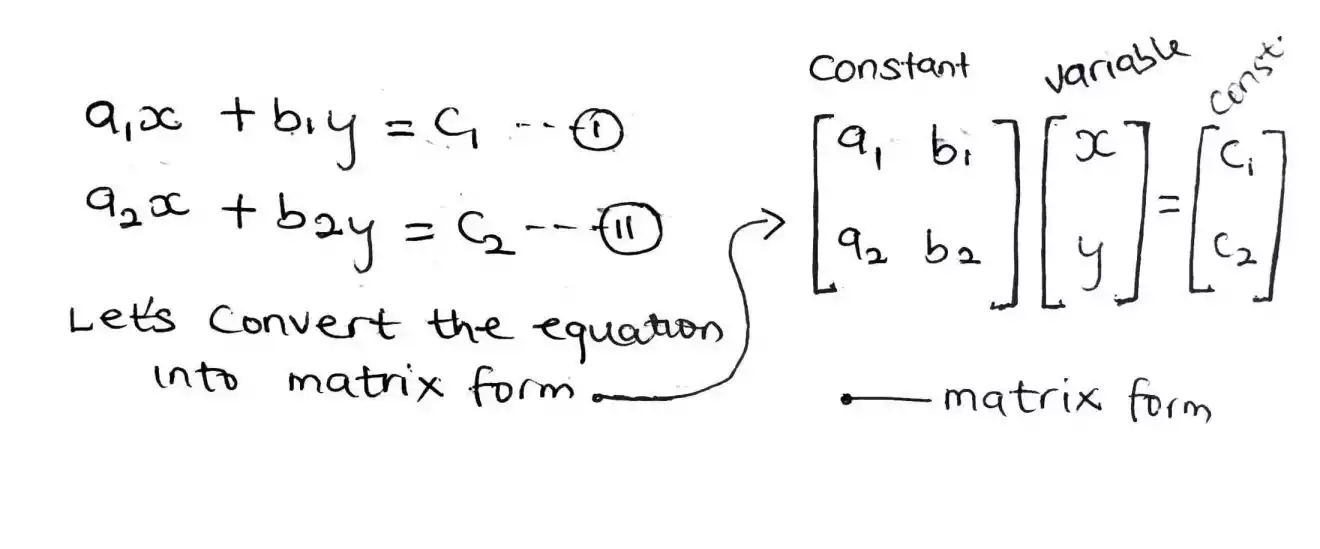
[a₁x + b₁y = c₁ ] and [a₂x + b₂y = c₂ ] Then we need to convert this equation into a rectangular matrix and then find the determinant of the matrix which is labelled as D, the determinant of the variable x labelled as Dx and that of y which is also labelled as Dy.

After finding this parameters, we can now solve for x and by using the following sets of formula.

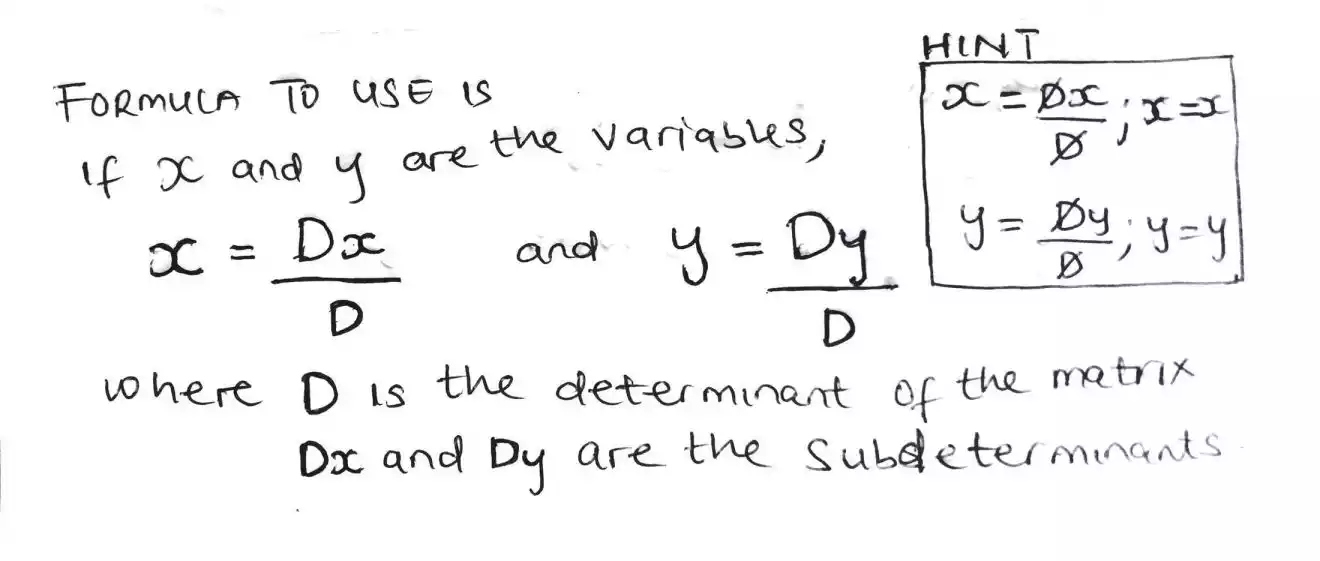
For example, if determinant is 4 (i.e. D = 4) and determinant of x is 8 (i.e. Dx = 8) therefore, x = 8/4 = 2 (i.e. x = Dx/D).

Small nugget

Tips to recall this formula is if we are looking for x then we need Dx first and divide by D, think of simple algebra. A visual hint is shown in the hint box above.

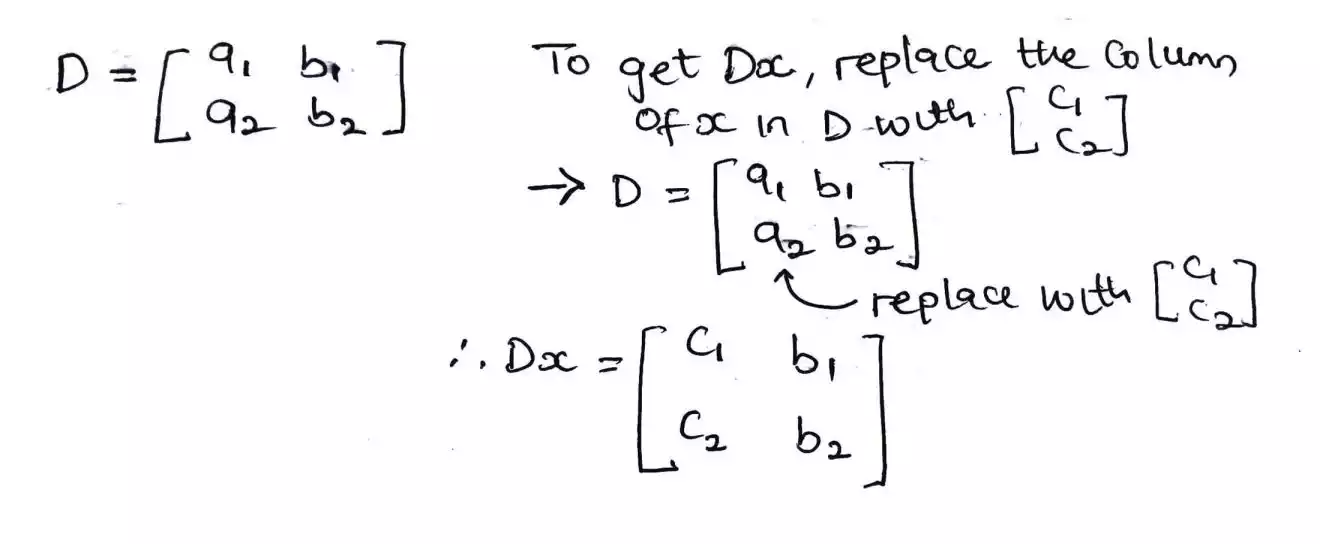
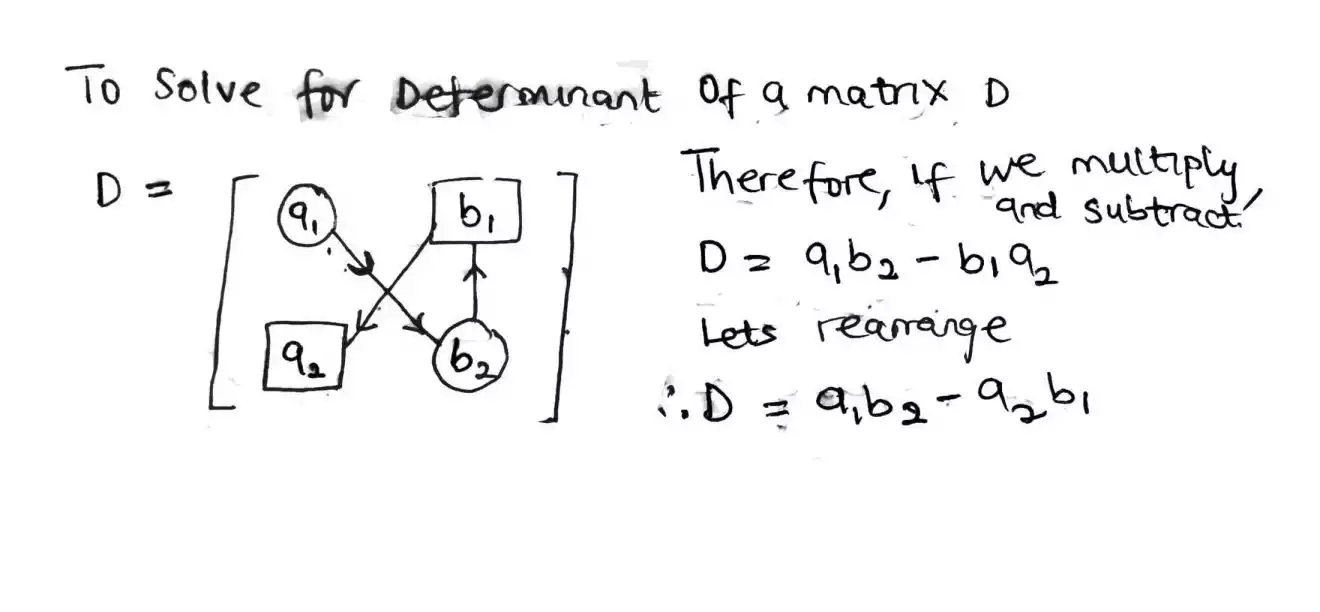
Let find what D is – D can be gotten by forming a rectangular matrix with the constant at the right hand side which are a₁, b₁, a₂ and b₂.

To find Dx, we replace the constant values that belong to the variable x in the D matrix with the constant value c₁ and c₂ in the right hand side.

Likewise, we replace the constant values that belong to the variable y in the D matrix with the constant value c₁ and c₂ in the right hand side to get Dy.

Let simplify but before then, if we have a 2x2 matrix, the way we solve them is, on the first row first column, take the value there and multiply it with the adjacent value so we have (a₁ x b₂). For the first row second column, we take it value and multiply it with the adjacent value also in order to have (b₁ x a₂) and then subtract the value from the previous value (a₁ x b₂) then we arrange it to make things simpler.

To find Dx and Dy, we follow the same format as above but don’t forget to replace the values beside the x variable with the constant value and y variable with the constant value also.

So we get something as shown below.

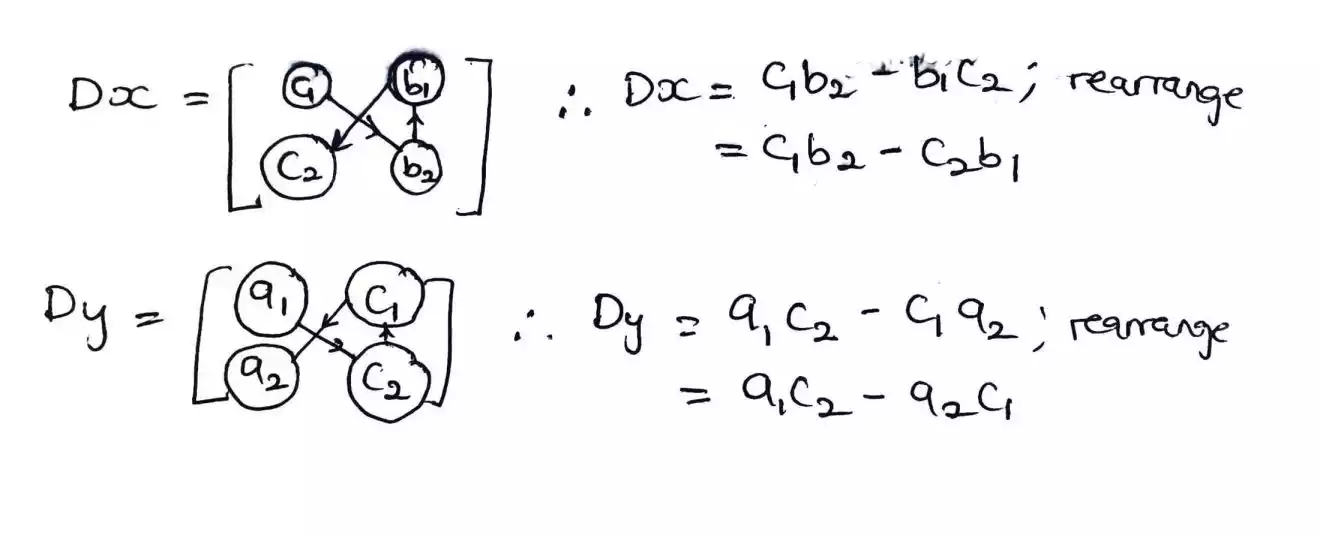
And lastly, we can get the value of x and y using our formula

Still if you want a proof for this using elimination by addition method for simultaneous equation then here it is.

Try it

Since the equation is a simultaneous equation, you can try this if you know how to use simultaneous equation to proof this out yourself.

To apply elimination by subtraction method, we need to determine what variable do we want to eliminate first and the one we needed since we can only find one variable at a time.

So let first eliminate x and find y. To eliminate x, multiply equation 1 through by the constant of x in equation two which is a2 and then multiply equation two by the constant of x in equation one which is a1 so that both side have same constant which will allow us to subtract them.

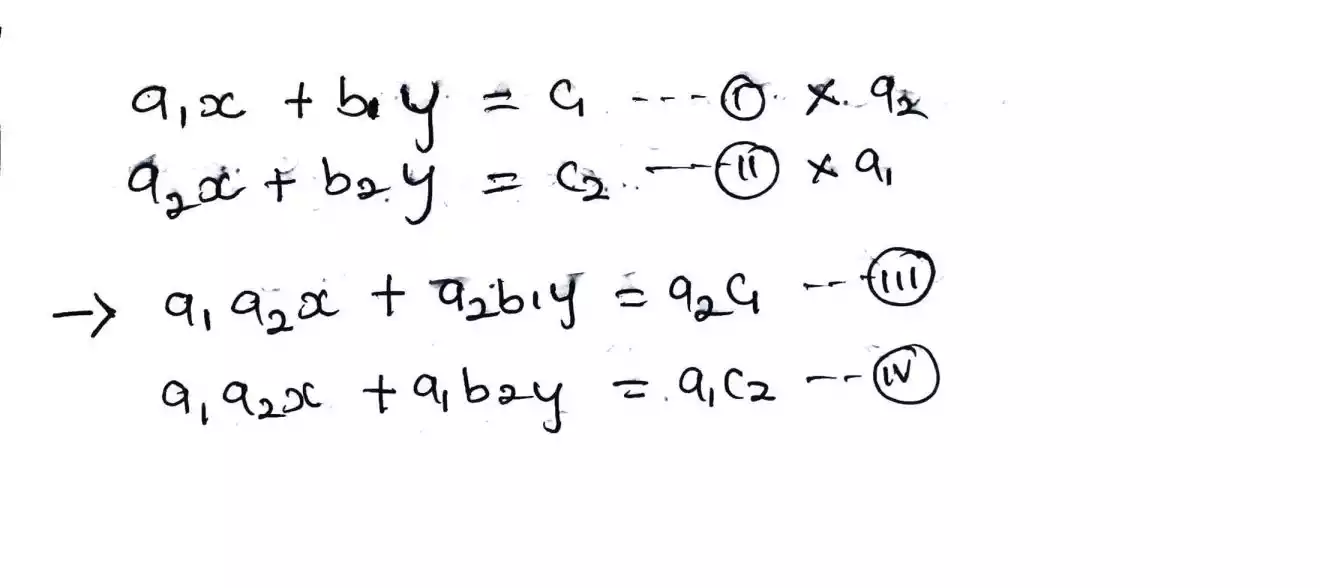
Then by subtracting them, our result is shown below

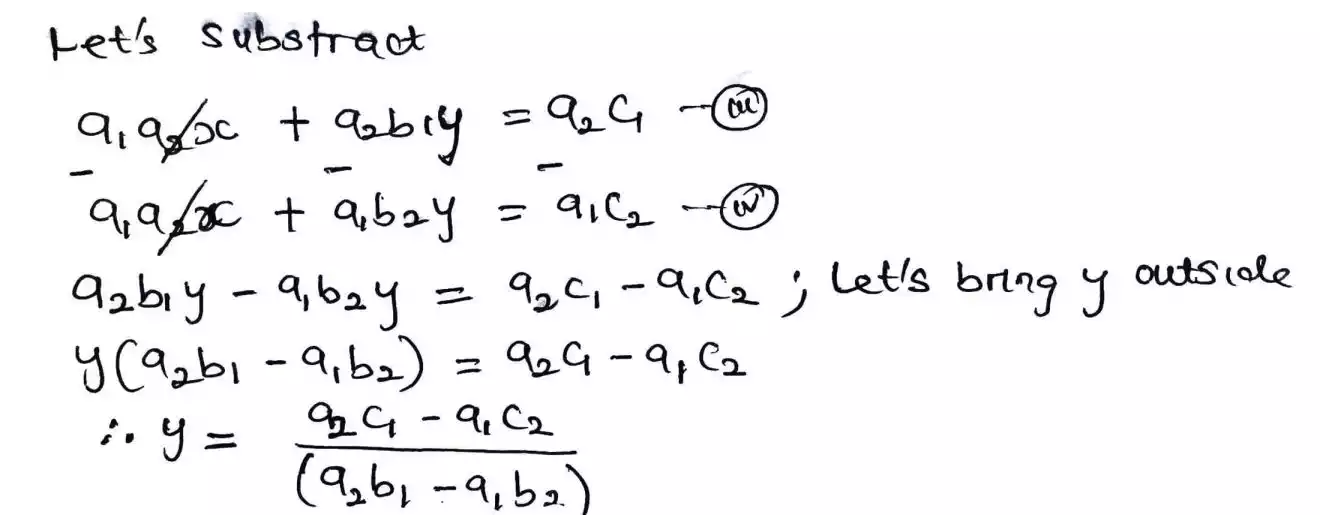
From the result shown, go look at what y is when we use crammer's rule and see if there is difference.

Oh yeah! there is because it doesn’t match right! This is just rearrangement issue so to fix that, if we multiply our equation both top and bottom by (-1), we will see an effect.

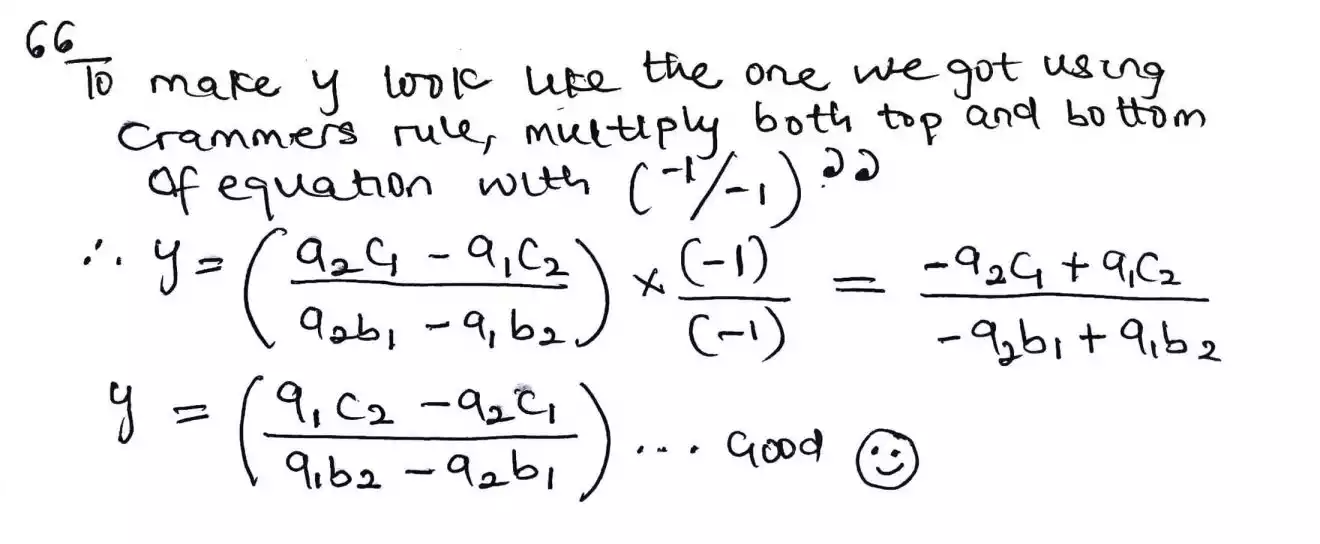
Note this (-1) one is not adding something new to our equation because, we are multiplying both top and bottom which still gives 1 and anything multiplied by one is the same. But we just need to do this to change sign.

We now see the difference between the two solutions by going further and rearranging again.

Lastly, like I said use any one you like but when it comes to more complicated equations like 3x3, crammer's rule will look much prettier – still it’s based on preference.

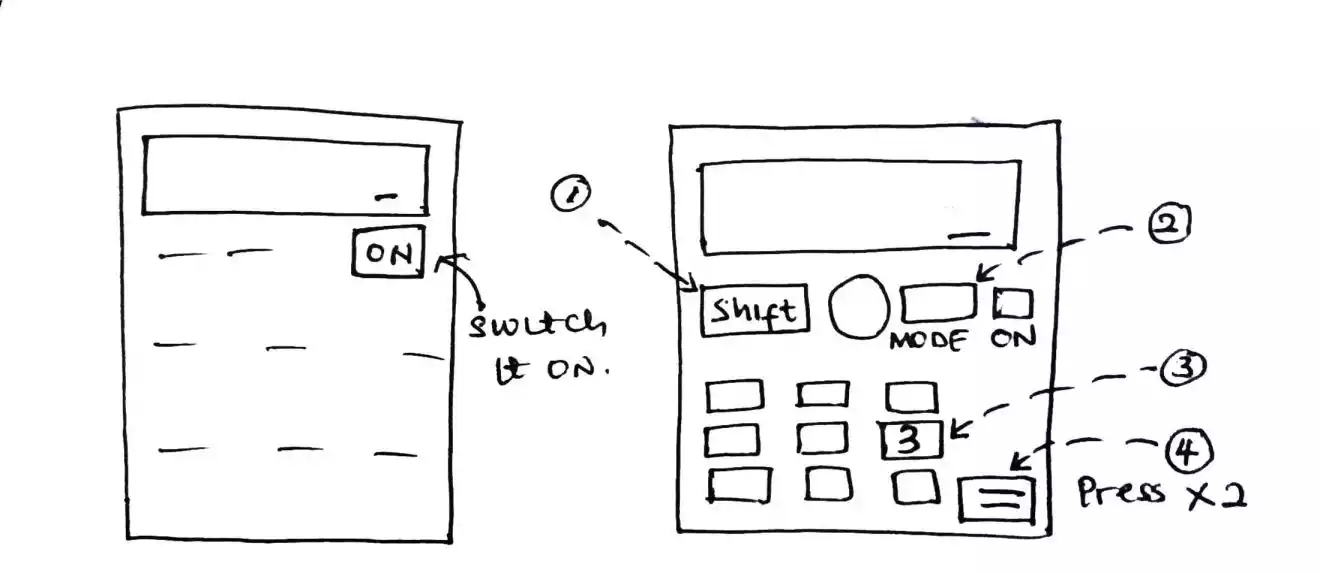
Once more and not to forget, if you would love to use a calculator to help you solve simultaneous equations fast then here is an article.