How to Multiply Two Polynomials in MATLAB?
Polynomial multiplication is a fundamental operation in algebra, and MATLAB provides a powerful tool to perform this operation efficiently.
In this article, we will look at how to multiply two polynomials using MATLAB, by using the function: conv().
Polynomial Multiplication: A Review
Before looking into how to use MATLAB to multiply polynomials together, let’s briefly review polynomial multiplication.
Given two polynomials:
$ P(x) = a_n x^n + a_{n-1} x^{n-1} + \ldots + a_1x + a_0 $
$Q(x) = b_m x^m + b_{m-1} x^{m-1} + \ldots + b_1 x + b_0$
The product of $P(x)$ and $Q(x)$, denoted as $ P(x) \cdot Q(x) $, is calculated by multiplying each term of the first polynomial by each term of the second polynomial and summing the results.
In mathematical terms, the product is:
$P(x) \cdot Q(x) = \sum_{i=0}^{n} \sum_{j=0}^{m} a_i b_j x^{i+j}$
How to use MATLAB conv() Function to Multiply Polynomials?
MATLAB simplifies the process of polynomial multiplication with the conv() function.
This function operates on two vectors, representing the coefficients of the polynomials, and returns the coefficients of their product.
Syntax of the function:
conv(p1, p2)
Arguments of the conv() function:
The “conv()” function takes two parameters; which are vectors that hold the coefficient of each polynomial.
p1: Represents the coefficient vector of the first polynomial.p2: Represents the coefficient vector of the second polynomial.
Return Value of the conv() function:
The result is a coefficient vector representing the product polynomial.
An Example Problem:
Let’s consider the following polynomials:
$P(x) = 1x^2 + 2x + 3 $
$Q(x) = 4x^2 + 5x + 6 $
If you want to multiply these two polynomials together, the MATLAB code is:
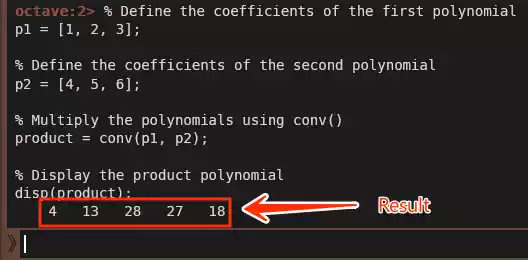
% Define the coefficients of the first polynomial
p1 = [1, 2, 3];
% Define the coefficients of the second polynomial
p2 = [4, 5, 6];
% Multiply the polynomials using conv()
product = conv(p1, p2);
% Display the product polynomial
disp(product);
The result of this code is the coefficient vector [4, 13, 28, 27, 18], representing the product polynomial:
Result: $ 4x^4 + 13x^3 + 28x^2 + 27x + 18$
Explanation of the MATLAB Code:
Firstly, the polynomial $P(x) = 1x^2 + 2x + 3$ is represented as a vector by extracting its coefficients.
This vector is stored in a variable named p1. In MATLAB syntax, it is defined as:
p1 = [1, 2, 3];
Similarly, the coefficients of the second polynomial $Q(x) = 4x^2 + 5x + 6$ are stored in another variable named p2:
p2 = [4, 5, 6];
Now, the convolution function conv() is used to multiply the two polynomials represented by the vectors p1 and p2.
The result is stored in a variable called product:
product = conv(p1, p2);
At this point, the product variable holds the coefficients of the product polynomial.
Finally, the disp() function is used to display the result on the screen:
disp(product);
The displayed result is the coefficient vector [4, 13, 28, 27, 18], which corresponds to the product polynomial:
$ 4x^4 + 13x^3 + 28x^2 + 27x + 18 $
Wrap Up
As a wrap up, to multiply polynomials in MATLAB using the conv() function, you start by defining coefficient vectors for each polynomial.
The conv() function then efficiently computes the product of the polynomials by convolving their coefficient vectors.





